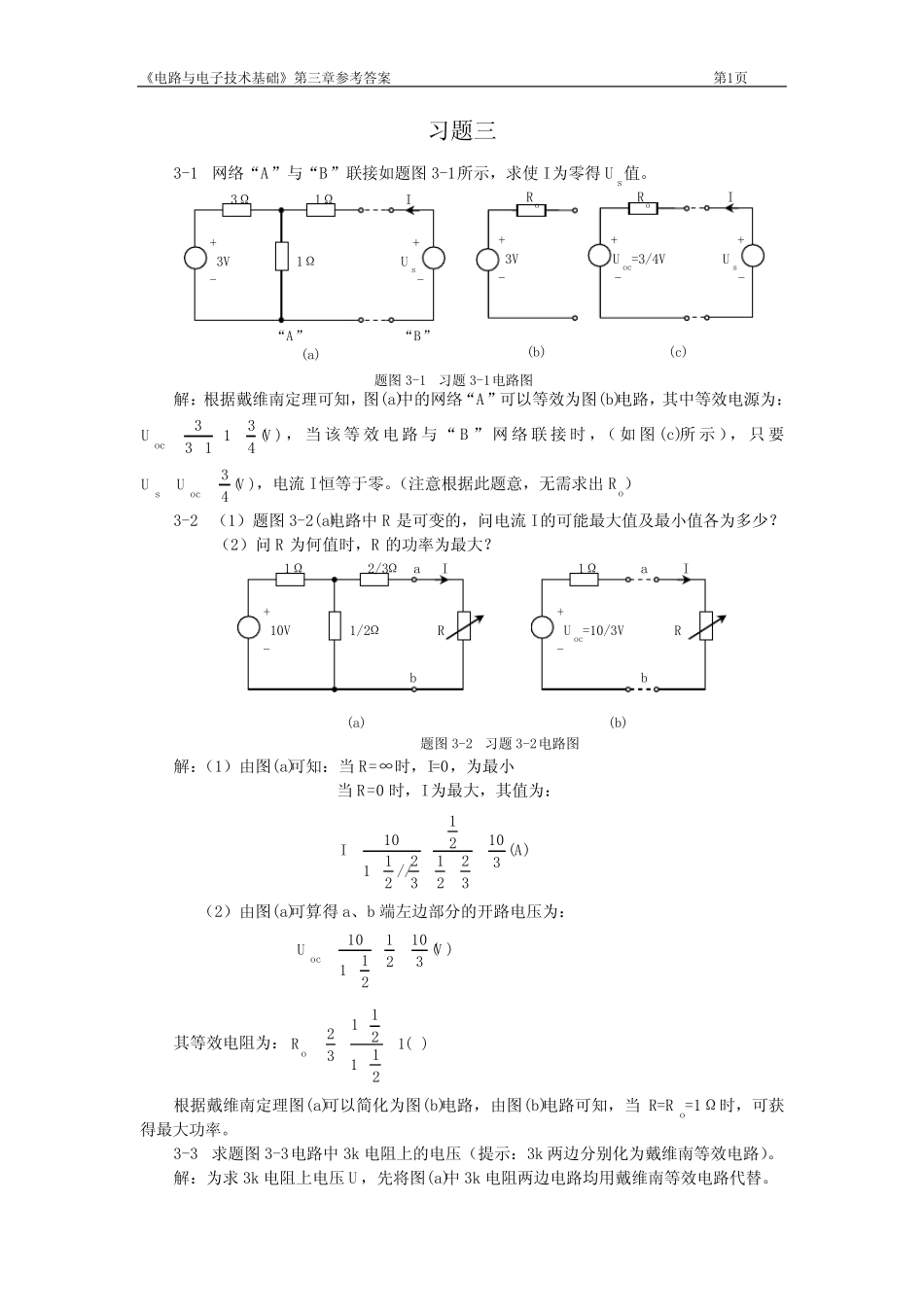
《 电 路 与 电 子 技 术 基 础 》 第 三 章 参 考 答 案 第 1页 习 题 三 3-1 网 络 “ A” 与 “ B” 联 接 如 题 图 3-1所 示 , 求 使 I为 零 得 U s值 。 解 : 根 据 戴 维 南 定 理 可 知 , 图 (a)中 的 网 络 “ A” 可 以 等 效 为 图 (b)电 路 , 其 中 等 效 电 源 为 :)(431133VU oc, 当 该 等 效 电 路 与 “ B ” 网 络 联 接 时 , ( 如 图 (c)所 示 ) , 只 要)(43 VUUocs, 电 流 I恒 等 于 零 。( 注 意 根 据 此 题 意 , 无 需 求 出 R o) 3-2 ( 1) 题 图 3-2(a)电 路 中 R 是 可 变 的 , 问 电 流 I的 可 能 最 大 值 及 最 小 值 各 为 多 少 ? ( 2) 问 R 为 何 值 时 , R 的 功 率 为 最 大 ? 解 :( 1) 由 图 (a)可 知 : 当 R=∞ 时 , I=0, 为 最 小 当 R=0 时 , I为 最 大 , 其 值 为 : )(31032212132//21110AI ( 2) 由 图 (a)可 算 得 a、 b 端 左 边 部 分 的 开 路 电 压 为 : )(3102121110VU oc 其 等 效 电 阻 为 :)(121121132oR 根 据 戴 维 南 定 理 图 (a)可 以 简 化 为 图 (b)电 路 , 由 图 (b)电 路 可 知 , 当R=R o=1Ω 时 , 可 获得 最 大 功 率 。 3-3 求 题 图 3-3电 路 中 3k 电 阻 上 的 电 压 ( 提 示 : 3k 两 边 分 别 化 为 戴 维 南 等 效 电 路 )。 解 : 为 求 3k 电 阻 上 电 压 U , 先 将 图 (a)中 3k 电 阻 两 边 电 路 均 用 戴 维 南 等 效 电 路 代 替 。 3Ω 1Ω I + + 3V 1Ω U s - - “ A” “ B” (a) R o R o I + + + 3V U oc=3/4V U s - - - (b) (c) 题 图 3-1 习 题 3-1电 路 图 1Ω 2/3Ω a I + 10V 1/2Ω R - b (a) 1Ω a I + U oc=10/3V R - b (b) 题 图 3-2 习 题 3-2电 路 图 《 电 路 与 电 子 技 术 基 础 》 第 三 章 参 考 答 案 第 2页 对 于 左 边 电 路 由 弥 尔 曼 定 理 有 : )(1060//30//20)(2030160120...