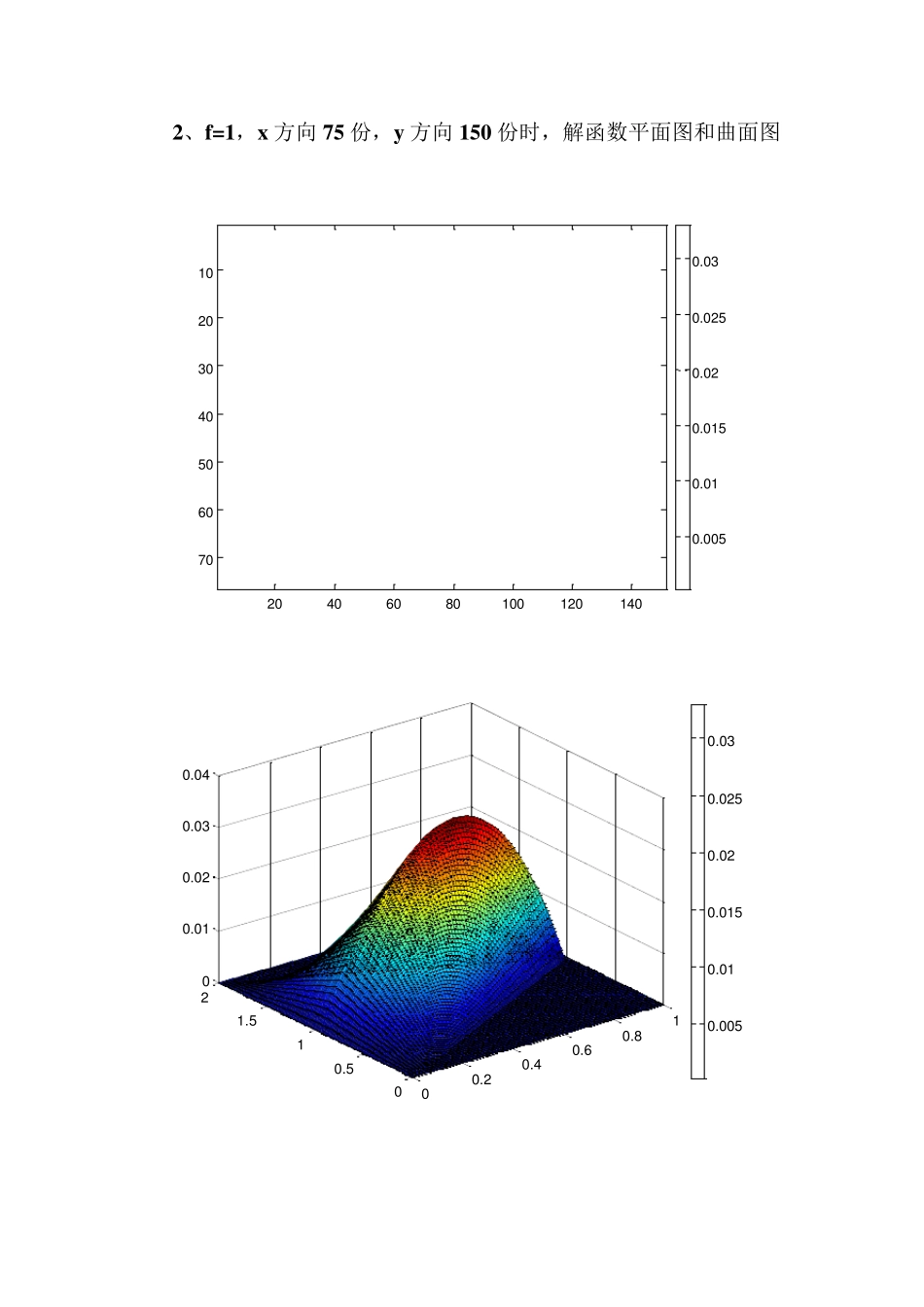
基于matlaB 编程的有限元法 一、待求问题: 泛定方程:2 =x 边界条件:以(0,-1),(0,1),(1,0)为顶点的三角形区域边界上 =0 二、编程思路及方法 1、给节点和三角形单元编号,并设定节点坐标 画出以(0,-1),(0,1),(1,0)为顶点的三角形区域 figu re1 由于积分区域规则,故采用特殊剖分单元,将区域沿水平竖直方向分等份,此时所有单元都是等腰直角三角形,剖分单元个数由自己输入,但竖直方向份数(用 Jmax 表示)必须是水平方向份数(Imax )的两倍,所以用户只需输入水平方向的份数 Imax 。 采用上述剖分方法,节点位置也比较规则。然后利用循环从区域内部(非边界)的节点开始编号,格式为 NN(i,j)=n1,i,j 分别表示节点所在列数与行数,并将节点坐标存入相应矩阵 X(n1),Y(n1)。由于区域上下两部分形状不同因此,分两个循环分别编号赋值,然后再对边界节点编号赋值。 然后再每个单元的节点进行局部编号,由于求解区域和剖分单元的特殊性,分别对内部节点对应左上角正方形的两个三角形单元,上左,左上,下斜边界节点要对应三个单元,上左,左上,左下,右顶点的左下、左上,右上边界的左上,分别编号以保证覆盖整个区域。 2 、求解泊松方程 首先一次获得每个单元节点的整体编号,然后根据其坐标求出每个三角形单元的面积。利用有限元方法的原理,分别求出系数矩阵和右端项,并且由于边界条件特殊,边界上=0,因此做积分时只需对场域单元积分而不必对边界单元积分。求的两个矩阵后很容易得到节点电位向量,即泊松方程的解。 3 、画解函数的平面图和曲面图 由节点单位向量得到,j 行i 列节点的电位,然后调用绘图函数 imagesc(NNV)与 surf(X1,Y1,NNV')分别得到解函数的平面图 figure2 和曲面图 figure3。 4 、将结果输出为文本文件 输出节点编号,坐标,电位值 三、计算结果 1 、积分区域: 00 .10 .20 .30 .40 .50 .60 .70 .80 .91-1-0 .8-0 .6-0 .4-0 .200 .20 .40 .60 .81 2、f=1,x 方向 75 份,y 方向 150 份时,解函数平面图和曲面图 2 04 06 08 01 0 01 2 01 4 01 02 03 04 05 06 07 00 .0 0 50 .0 10 .0 1 50 .0 20 .0 2 50 .0 3 00 .20 .40 .60 .8100 .511 .5200 .0 10 .0 20 .0 30 .0 40 .0 0 50 .0 10 .0 1 50 .0 20 .0 2 50 .0 3 对比:当f=1 时,界函数平面图 2 04...