函数的凸性曲线的曲率VIP免费

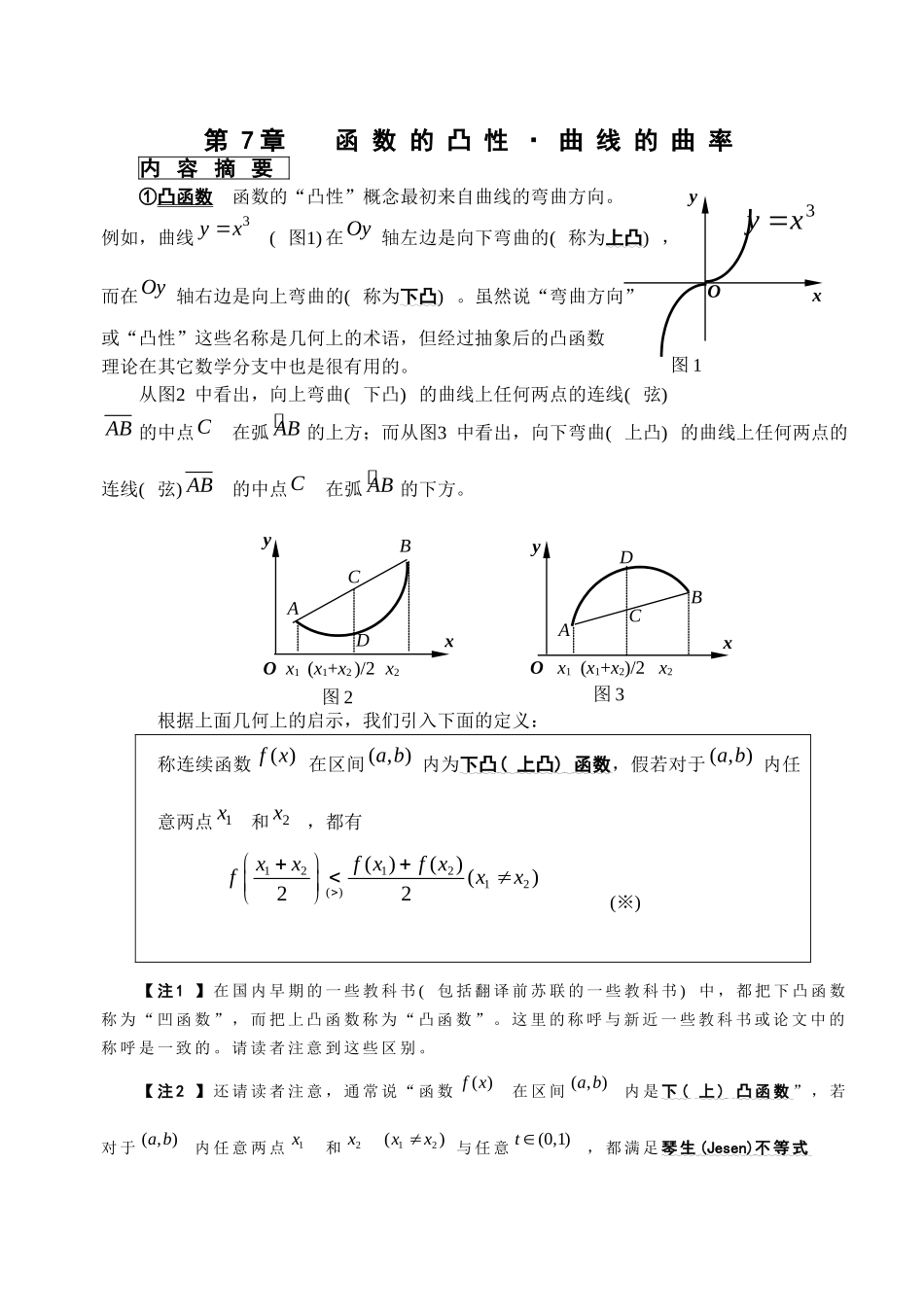
第7章函数的凸性·曲线的曲率内容摘要①凸函数函数的“凸性”概念最初来自曲线的弯曲方向。例如，曲线3xy(图1)在Oy轴左边是向下弯曲的(称为上凸)，而在Oy轴右边是向上弯曲的(称为下凸)。虽然说“弯曲方向”或“凸性”这些名称是几何上的术语，但经过抽象后的凸函数理论在其它数学分支中也是很有用的。从图2中看出，向上弯曲(下凸)的曲线上任何两点的连线(弦)AB的中点C在弧AB的上方；而从图3中看出，向下弯曲(上凸)的曲线上任何两点的连线(弦)AB的中点C在弧AB的下方。根据上面几何上的启示，我们引入下面的定义：称连续函数)(xf在区间),(ba内为下凸(上凸)函数，假若对于),(ba内任意两点1x和2x，都有121212()()()()22xxfxfxfxx(※)【注1】在国内早期的一些教科书(包括翻译前苏联的一些教科书)中，都把下凸函数称为“凹函数”，而把上凸函数称为“凸函数”。这里的称呼与新近一些教科书或论文中的称呼是一致的。请读者注意到这些区别。【注2】还请读者注意，通常说“函数()fx在区间(,)ab内是下(上)凸函数”，若对于(,)ab内任意两点1x和2x12()xx与任意(0,1)t，都满足琴生(Jesen)不等式图2ABCDxyOx1(x1+x2)/2x2yABCD图3Ox1(x1+x2)/2x2x图13xyxyO1212()(1)()(1)()ftxtxtfxtfx它等价于不等式11221122()()()ftxtxtfxtfx（其中1t和2t为正数且121tt）显然，不等式(※)是琴生不等式的特殊情形。不过，对于连续函数来说，不等式(※)与琴生不等式是等价的。因此，我们就用简单的不等式(※)定义函数的凸性。关于连续函数情形下两者等价性的证明，有兴趣的读者可去看本网站上的专题选讲。【注3】若函数)(xf在区间),(ba内可微分，则从下图4看出，下凸(上凸)函数的图形上，每一点处的切线都在图形的下面(上面)，而且导函数)(xf(切线的斜率)是增大(减小)的。我们也可以证明这个结论(见专题选讲)。定理设函数)(xf在区间),(ba内有导数。若导数)(xf在),(ba内是增大(减小)的，则函数)(xf在区间),(ba内是下凸(上凸)的。(逆命题也成立。专题选讲中有证明)。假若函数)(xf在区间(,)ab内有二阶导数，那么根据上述定理和判别函数单调性的方法，就有下面判别函数凸性的方法。判别法设函数)(xf在区间),(ba内有二阶导数)(xf⑴若()0()fxaxb，则)(xf在区间),(ba内是下凸函数[因为导数)(xf是增函数]；⑵若()0()fxaxb，则)(xf在区间),(ba内是上凸函数[因为导数)(xf是108图4①下凸切线②上凸切线减函数]。②拐点(变曲点)函数图形可能在这一段上是上凸的，而在相邻的另一段上又是下凸的(如图1中原点的两边)。这样两段弧的连接点，就称为函数图形(曲线)的拐点(曲线拐弯的点)或变曲点(曲线改变弯曲方向的点)。同时，也把函数图形拐点的横坐标称为这个函数的拐点或变曲点。请读者注意到函数的拐点与函数图形(曲线)的拐点之间的区别!若点0(,)xab是函数()fx的拐点且有二阶导数0()fx，则00()fx这是因为，例如函数)(xf在点0x的左边近旁下凸时，由于00()()()fxfxxx(见注3)，所以0)()(lim)(0000xxxfxfxfxx(极限运算单调性)且函数)(xf在点0x的右边上凸时，由于)()()(00xxxfxf，所以0)()(lim)(0000xxxfxfxfxx(极限运算单调性)因此0()0fx.同理，若函数)(xf在点0x的左边上凸且在点0x的右边下凸时，也有0)(0xf.但是要注意，仅有0)(0xf时，点0x不一定是函数)(xf的拐点。例如函数4()fxx，尽管有(0)0f，但0不是函数4()fxx的拐点，因为2()120(||0)fxxx即函数4()fxx在原点0的两边都是下凸的(图5)。特别，假若函数()fx在区间00(,)xx内有二阶导数,且()fx在点0x的两边有相反的符号,则0x就是函数()fx的拐点。此时，当然有0)(0xf③勾画函数图形的方法在中学数学中，画函数图形用的是描点法。它的缺点是不能从整体上把握函数变化的状109图5Oxy4yx态。微积分中讲的绘图方法称为解析法，而它的优点正好弥补了描点法的缺陷。我们利用导数的有关信息所画出的略图，使我们能够看出函数的变化状态。例如在哪个区...