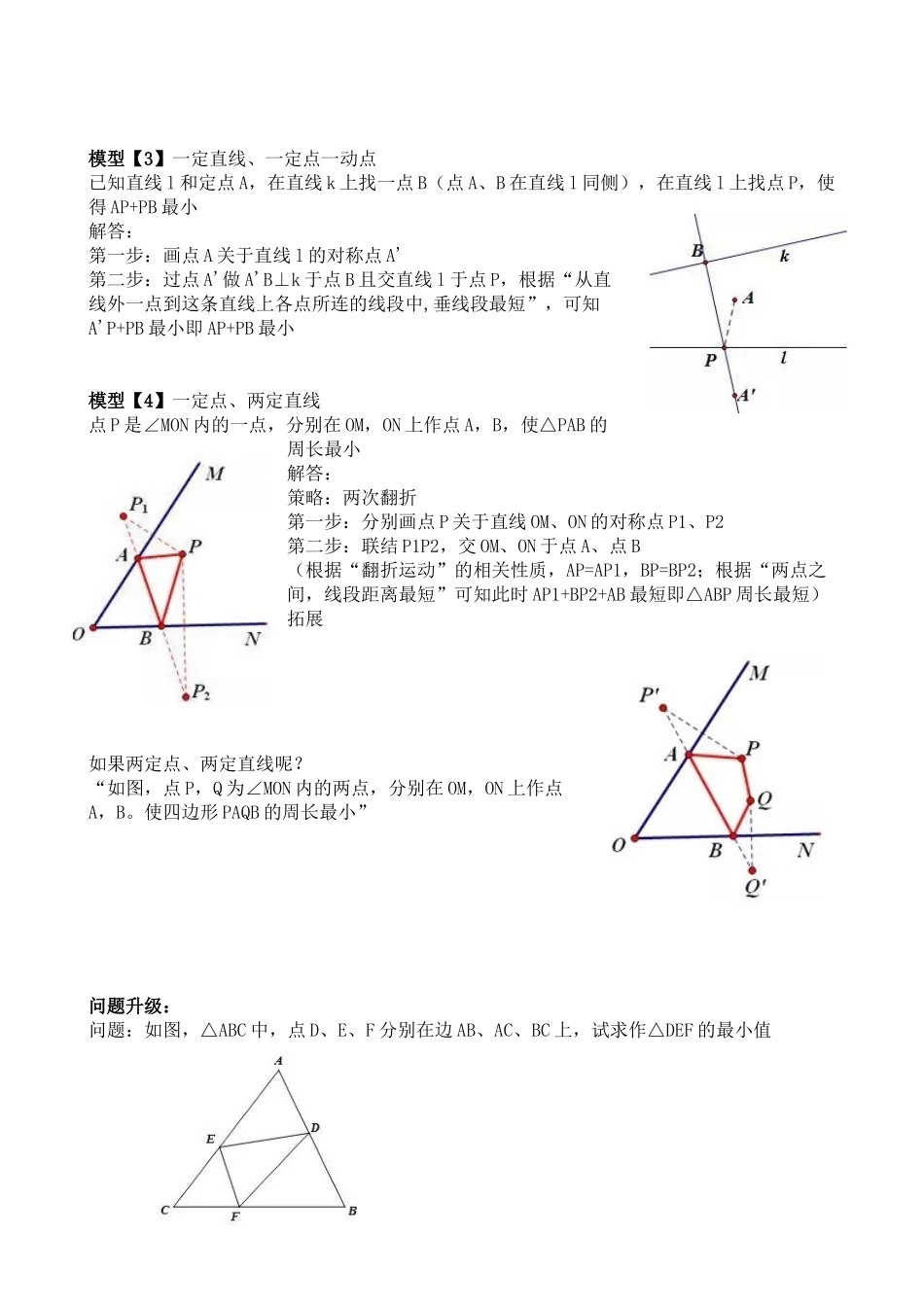
“将军饮马”模型详解与拓展平面几何中涉及最值问题的相关定理或公理有:① 线段公理:两点之间,线段最短. 并由此得到三角形三边关系; ② 垂线段的性质:从直线外一点到这条直线上各点所连的线段中,垂线段最短. 在一些“线段和最值”的问题中,通过翻折运动,把一些线段进行转化即可应用 ①、② 的基本图形,并求得最值,这类问题一般被称之为“将军饮马”问题。问题提出:唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题.如图所示,诗中将军在观望烽火之后从山脚下的 A 点出发,走到河边饮马后再到 B 点宿营.请问怎样走才能使总的路程最短?模型提炼:模型【1】一定直线、异侧两定点直线 l 和 l 的异侧两点 A、B,在直线 l 上求作一点 P,使 PA+PB 最小解答:根据“两点之间,线段距离最短”,所以联结 AB 交直线 l 于点 P,点 P 即为所求点模型【2】一定直线、同侧两定点直线 l 和 l 的同侧两点 A、B,在直线 l 上求作一点 P,使 PA+PB 最小解答:第一步:画点 A 关于直线 l 的对称点 A'(根据“翻折运动”的相关性质,点 A、A'到对称轴上任意点距离相等,如图所示,AP=A'P,即把一定直线同侧两定点问题转化为一定直线异侧两定点问题)第二步:联结 A'B 交直线 l 于点 Q,根据“两点之间,线段距离最短”,此时“A'Q+QB”最短即“AQ+QB”最短模型【3】一定直线、一定点一动点已知直线 l 和定点 A,在直线 k 上找一点 B(点 A、B 在直线 l 同侧),在直线 l 上找点 P,使得 AP+PB 最小解答:第一步:画点 A 关于直线 l 的对称点 A'第二步:过点 A'做 A'B⊥k 于点 B 且交直线 l 于点 P,根据“从直线外一点到这条直线上各点所连的线段中,垂线段最短”,可知A'P+PB 最小即 AP+PB 最小模型【4】一定点、两定直线点 P 是∠MON 内的一点,分别在 OM,ON 上作点 A,B,使△PAB 的周长最小解答:策略:两次翻折第一步:分别画点 P 关于直线 OM、ON 的对称点 P1、P2第二步:联结 P1P2,交 OM、ON 于点 A、点 B(根据“翻折运动”的相关性质,AP=AP1,BP=BP2;根据“两点之间,线段距离最短”可知此时 AP1+BP2+AB 最短即△ABP 周长最短)拓展如果两定点、两定直线呢?“如图,点 P,Q 为∠MON 内的两点,分别在 OM,ON 上作点A,B。使四边形 PAQB 的周长最小”问题升级:问...