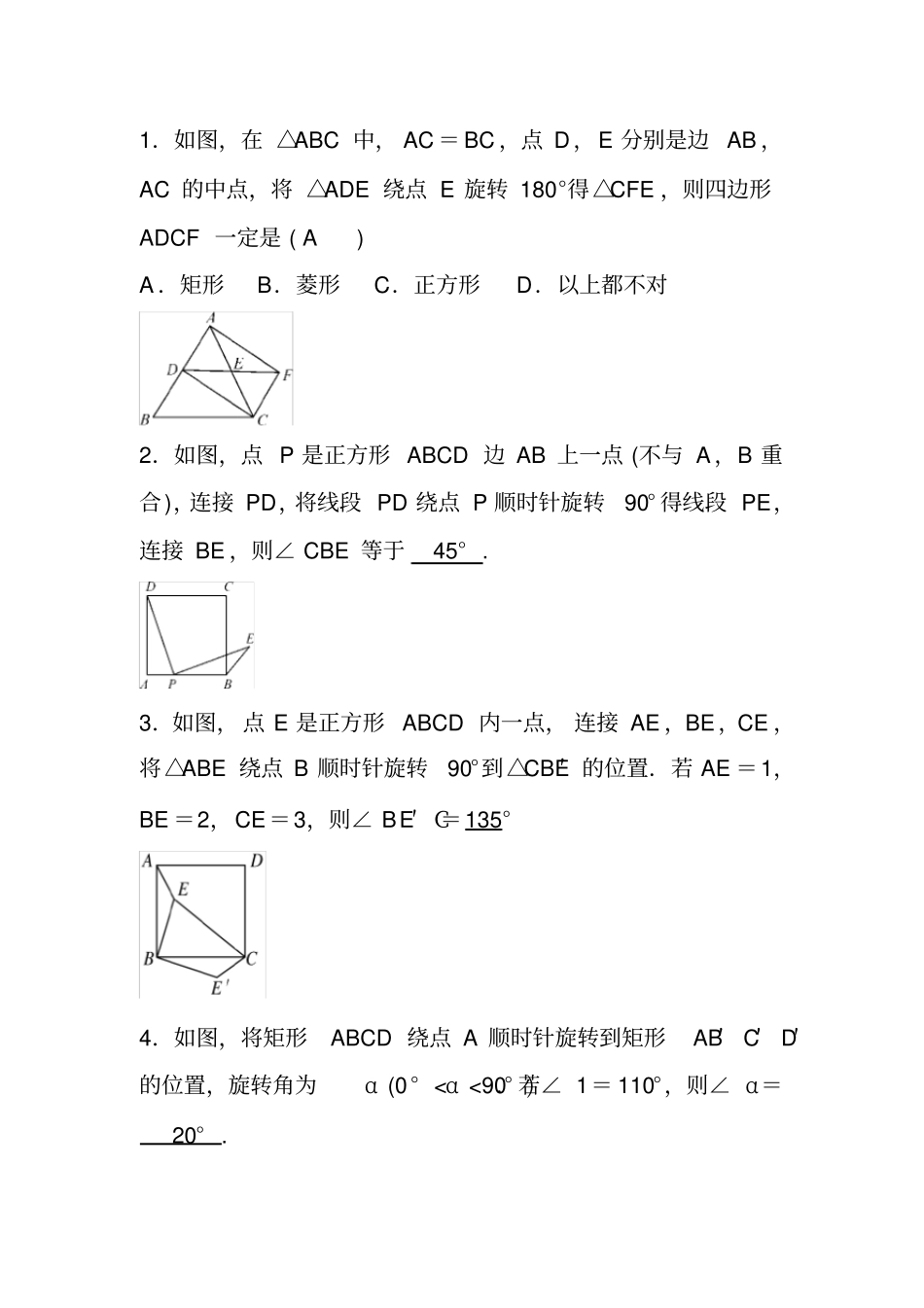
1.如图,在 △ABC 中, AC = BC ,点 D,E 分别是边 AB ,AC 的中点,将 △ADE 绕点 E 旋转 180°得△CFE ,则四边形ADCF 一定是 ( A ) A .矩形B.菱形C.正方形D.以上都不对2.如图,点 P 是正方形 ABCD 边 AB 上一点 (不与 A ,B 重合),连接 PD,将线段 PD 绕点 P 顺时针旋转90° 得线段 PE,连接 BE ,则∠ CBE 等于45° . 3.如图, 点 E 是正方形 ABCD 内一点, 连接 AE ,BE,CE ,将△ABE 绕点 B 顺时针旋转90°到△CBE′ 的位置.若 AE =1,BE =2,CE=3,则∠ BE′ C=135°4.如图,将矩形ABCD 绕点 A 顺时针旋转到矩形AB′C′D′的位置,旋转角为α (0 ° <α <90° ).若∠ 1= 110°,则∠ α=20° . DCBAO5.如图 8,A、B、C、D 四个点在同一个圆上,四边形 ABCD 的对角线把四个内角分成的八个角中,相等的角有 ( C) A.2 对B.3 对C.4 对D.5 对6.如图 ,∠AOB=100° ,则∠ A+ ∠B 等于 ( C ) A.100 °B.80 °C.50 °D.40 °7.如图 ,A、B、C 三点都在⊙ O 上,点 D 是 AB 延长线上一点 ,∠AOC=140°, ∠CBD 的度数是 ( C ) A.40 °B.50 °C.70 °D.110 °8.如图 ,AB为半圆O 的直径 ,弦 AD 、 BC 相交于点P,若CD=3,AB=4, 求 tan∠BPD 的值 . DCBPAO连接 BD, 则∴ AB 是直径 ,∴∠ ADB=90°. ∠ C= ∠A,∠D=∠ B,∴△ PCD ∽△ PAB, ∴ PDCDPBAB . DCBAOCBAO在 Rt △PBD 中,cos∠BPD= PDCDPBAB = 34 , 设 PD=3x,PB=4x, 则 BD=2222(4 )(3 )7PBPDxxx, ∴tan∠BPD=7733BDxPDx. 一、特殊的平行四边形动点问题1.如图,在 Rt △ABC 中,∠ ACB =90°,过点 C 的直线 MN∥AB ,D 为 AB 上一动点, 过点 D 作 DE ⊥BC ,交直线 MN于点 E,垂足为点F,连接 CD ,BE. (1)求证: CE=AD ;(2)当 D 运动到 AB 的中点时,四边形BECD 是什么特殊四边形?说明你的理由;(3)若 D 运动到 AB 的中点,则∠ A 的大小满足什么条件时,四边形 BECD 是正方形?说明你的理由.解: (1)证明: DE⊥ BC,∴∠ DFB =90° . ∠ ACB =90° ,∴∠ ACB =∠ DFB ,∴ AC ∥ DE. MN ∥AB ,即 CE∥AD ,∴四边形 ADEC 是平行四边形,∴CE =AD (2)四边形 BECD 是菱形,理由: D 为 AB 的中点,∴ AD=BD....