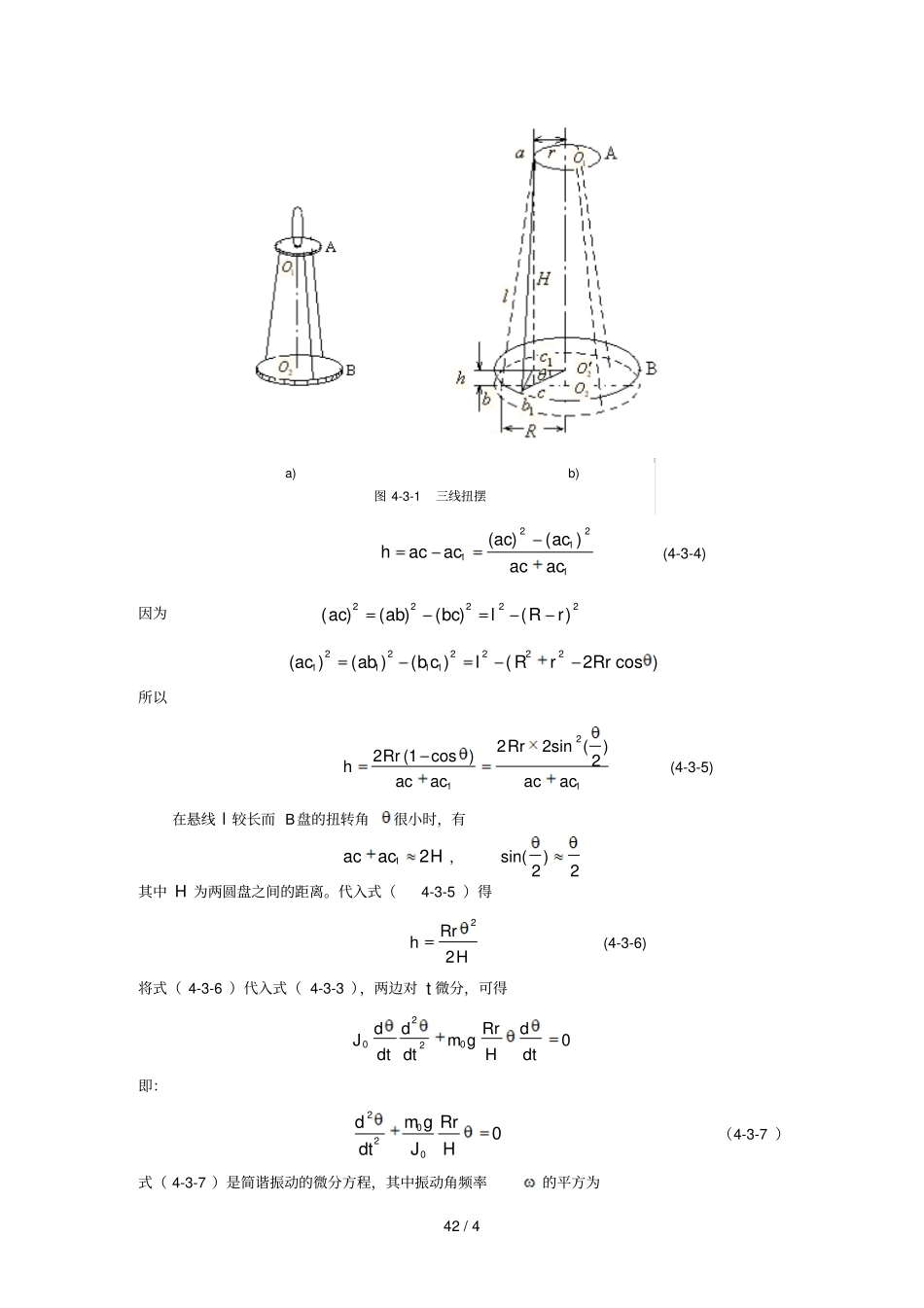
41 / 4 实验 4-3 用三线扭摆法测定物体的转动惯量转动惯量是刚体转动惯性大小的量度,它与刚体的质量、 转轴位置及质量相对转轴的分布情况有关。 对于形状简单规则的刚体,测出其尺寸和质量, 可用数学方法计算出转动惯量,而对形状复杂的刚体用数学方法求转动惯量非常困难,一般要通过实验方法来测定。三线扭摆法测转动惯量是一种简单易行的方法。【实验目的】 1.学会使用三线扭摆法测定圆盘和圆环绕其对称轴的转动惯量。2.学习使用MUJ-5B计时计数测速仪测量周期。3.研究转动惯量的叠加原理及应用。【实验器材】三线扭摆、钢直尺、游标卡尺、水准仪、钢圆环、铝圆环、MUJ-5B计时计数测速仪。【实验原理】三线扭摆装置如图4-3-1a所示。上、下两个圆盘均处于水平,圆盘A 的中心悬挂在支架的横梁上, 圆盘 B由三根等长的弦线悬挂在A 盘上。三条弦线的上端和下端分别在A圆盘和 B 圆盘上各自构成等边三角形,且两个等边三角形的中心与两个圆盘的圆心重合。A盘可绕自身对称轴12O O 转动,若将A 盘转动一个不大的角度,通过弦线作用将使B 盘摆动, B盘一方面绕轴12O O 转动,同时又在铅直方向上做升降平动,其摆动周期与B 盘的转动惯量大小有关。设 B 盘的质量是0m ,当它从平衡位置开始向某一方向转动角度时,上升高度为 h(如图 4-3-1b 所示),那么 B 盘增加的势能为pE0m gh (4-3-1) 这时 B 圆盘的角速度为ddt,B 盘的动能为201()2KdEJdt (4-3-2) 式中0J 是 B 盘绕自身中心轴的转动惯量。如果略去摩擦力,则圆盘系统的机械能守恒,即2001()2dJm ghdt常量 (4-3-3) 设悬线长为 l ,上圆盘悬线到盘心的距离为r ,下圆盘悬线到盘心的距离为R 。当下圆盘 B 转一小角度(05 )时,圆盘上升高度h ,从上盘 a 点向下作垂线,与升高前、后的下盘分别交于 c 、1c ,悬线端点 b 移到位置1b ,因而下盘B 上升高度为42 / 4 1hacac1212)()(acacacac (4-3-4) 因为22222()()()()acabbclRr222111 1()()()acabb c222(2cos )lRrRr所以21122sin ()2(1cos )2RrRrhacacacac (4-3-5) 在悬线 l 较长而 B盘的扭转角很小时,有12acacH ,sin()22其中 H 为两圆盘之间的距离。代入式(4-3-5 )得22RrhH (4-3-6) 将式( 4-3-6 )代入式( 4-3-3 ),两边对 t 微分,可得20020ddRrdJm gdt dtHdt即:20200m gdRrdtJH(4-3-7 )式( 4-3-7 )是简谐振动的微分方程,其中振动角频率...