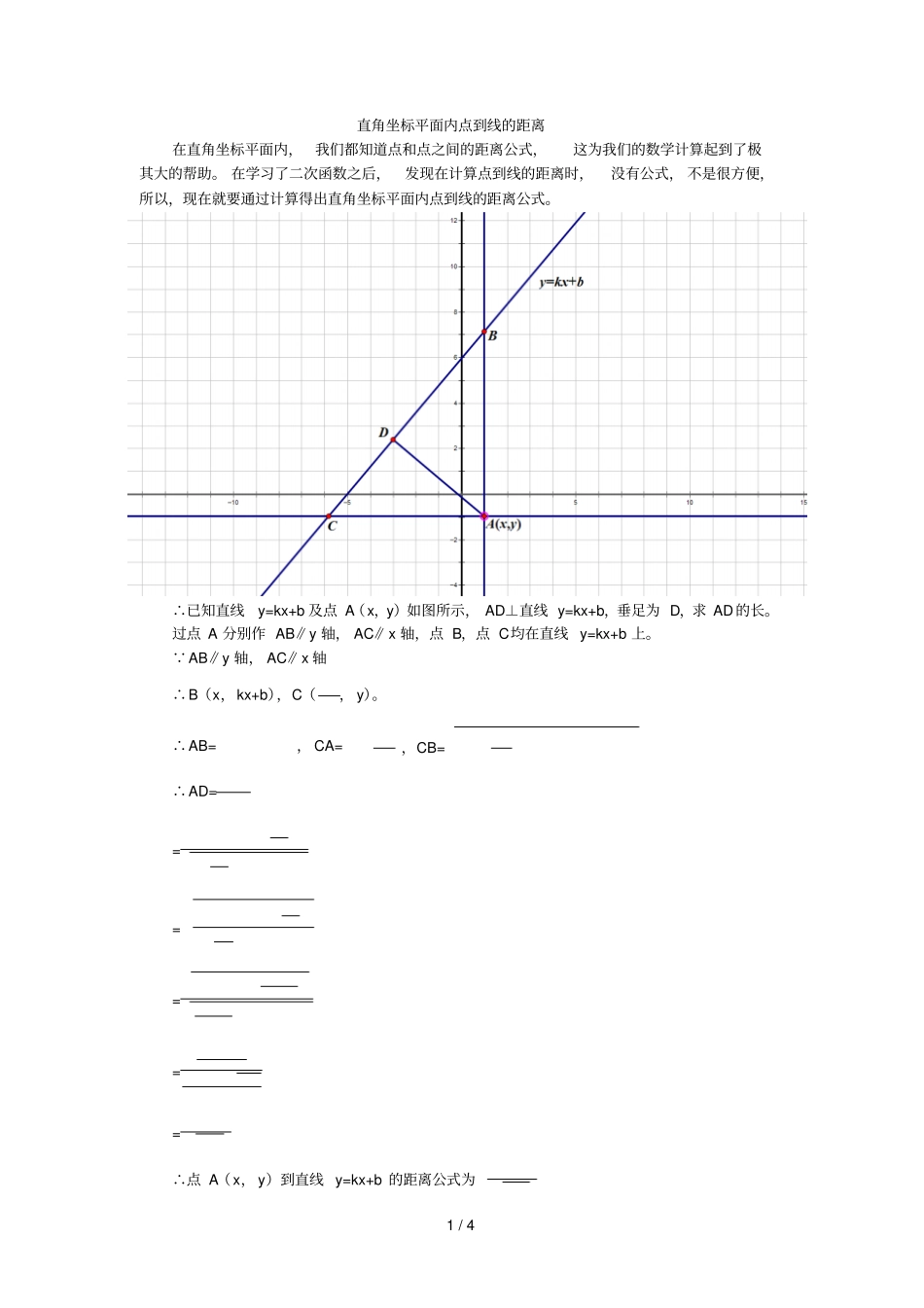
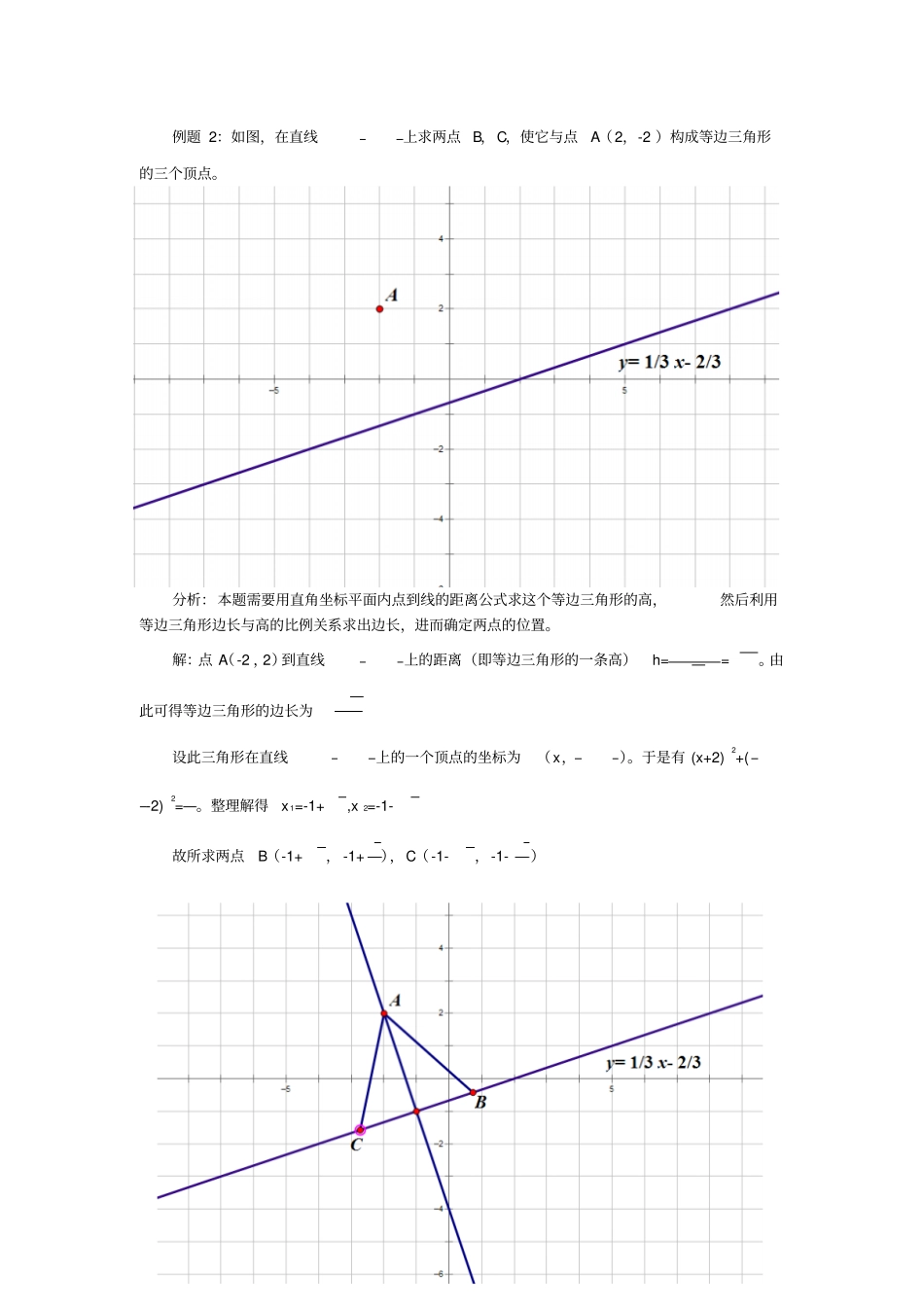
1 / 4 直角坐标平面内点到线的距离在直角坐标平面内,我们都知道点和点之间的距离公式,这为我们的数学计算起到了极其大的帮助。 在学习了二次函数之后,发现在计算点到线的距离时,没有公式, 不是很方便,所以,现在就要通过计算得出直角坐标平面内点到线的距离公式。∴已知直线y=kx+b 及点 A(x,y)如图所示, AD⊥直线 y=kx+b,垂足为 D,求 AD的长。过点 A 分别作 AB∥y 轴, AC∥x 轴,点 B,点 C均在直线 y=kx+b 上。∵AB∥y 轴, AC∥x 轴∴B(x,kx+b),C(, y)。∴AB=, CA=,CB=∴AD======∴点 A(x, y)到直线 y=kx+b 的距离公式为2 / 4 这个公式的得出可以让我们在解一些直角坐标系内的题目时可以更加方便,以下就是几个运用到直角坐标平面内点到线的距离公式的例题。例题 1;已知 A(-2 , -3 ),B(2,-1 ),C(0,2 ),求△ ABC的面积分析:如果没有直角坐标平面内点到线的距离公式,那么解这一道题需要用一个梯形的面积减去两个小三角形的面积,列式计算较为繁琐。但是如果用上这个距离公式,可以简化解题的过程,同时也可以提高准确率。解:由 A,B 两点坐标可得直线AB的解析式为y= x-2 ,同时可以求出AB的长度为 2。又已知 C的坐标(0,2 ),则可以算出C点与直线 AB的距离 h(即△ ABC AB边上的高)为=。可得 S△ABC=×2=8 例题 2:如图,在直线上求两点 B,C,使它与点A(2,-2 )构成等边三角形的三个顶点。分析:本题需要用直角坐标平面内点到线的距离公式求这个等边三角形的高,然后利用等边三角形边长与高的比例关系求出边长,进而确定两点的位置。解:点 A(-2 ,2)到直线上的距离(即等边三角形的一条高)h==。由此可得等边三角形的边长为设此三角形在直线上的一个顶点的坐标为(x,)。于是有 (x+2)2+(-2)2=。整理解得x 1=-1+,x 2=-1-故所求两点B(-1+, -1+),C(-1-,-1-)4 / 4 由此可以看出, 直角坐标平面内点到线的距离公式的作用是非常大的,以上列举的都是一些基础题, 在解一些综合题的时候,同样可以使用这个公式,可以大大提高做题的速度以及准确度。陈宇轩