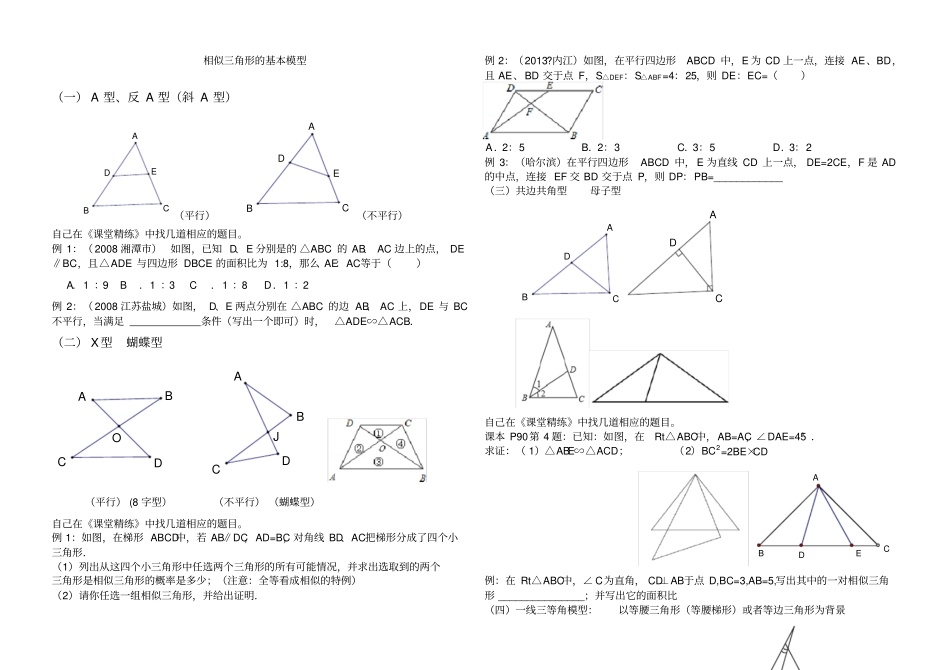
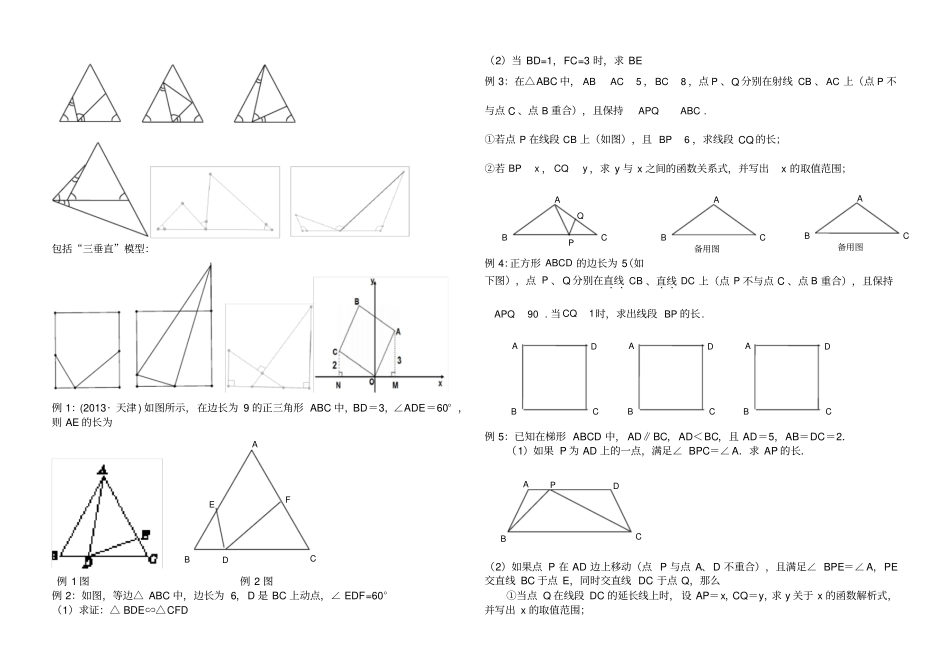
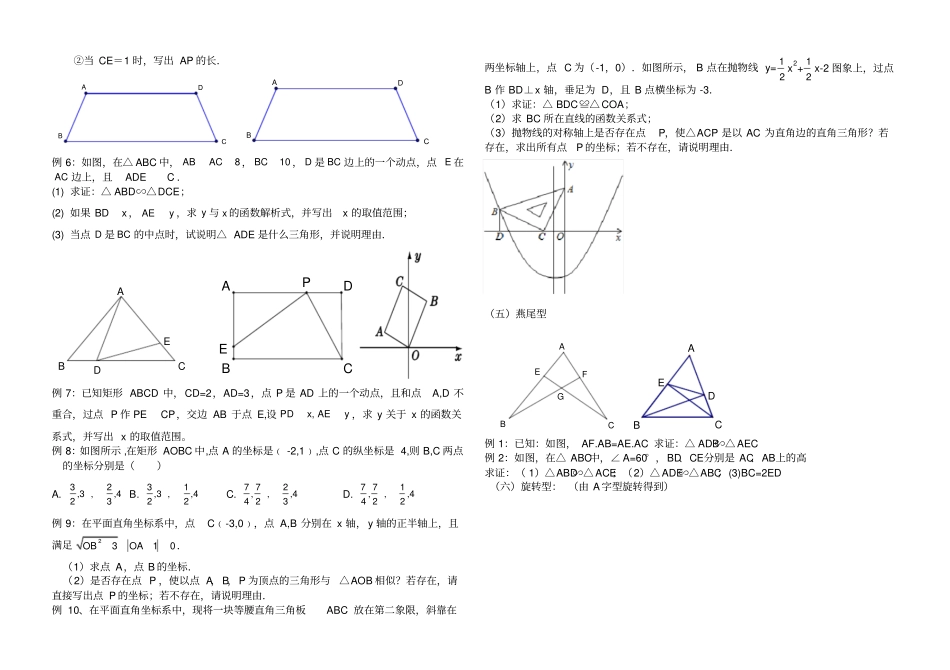
相似三角形的基本模型(一) A 型、反 A 型(斜 A 型)ABCDE(平行)CBADE(不平行)自己在《课堂精练》中找几道相应的题目。例 1:( 2008 湘潭市)如图,已知 D、E 分别是的 △ABC 的 AB、 AC 边上的点, DE∥BC,且△ADE 与四边形 DBCE 的面积比为 1:8,那么 AE:AC等于()A.1 : 9 B.1 : 3 C.1 : 8 D.1 : 2 例 2:( 2008 江苏盐城)如图, D、E 两点分别在 △ABC 的边 AB、 AC 上,DE 与 BC不平行,当满足条件(写出一个即可)时,△ADE∽△ACB.(二) X型蝴蝶型JOADBCABCD(平行) (8 字型)(不平行) (蝴蝶型)自己在《课堂精练》中找几道相应的题目。例 1:如图,在梯形 ABCD中,若 AB∥DC,AD=BC,对角线 BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.例 2:(2013?内江)如图,在平行四边形ABCD 中,E 为 CD 上一点,连接 AE、BD,且 AE、BD 交于点 F,S△DEF:S△ABF=4:25,则 DE:EC=()A.2:5 B.2:3 C.3:5 D.3:2 例 3:(哈尔滨)在平行四边形ABCD 中, E 为直线 CD 上一点, DE=2CE,F 是 AD的中点,连接 EF 交 BD 交于点 P,则 DP:PB=____________ (三)共边共角型母子型ABCDCAD自己在《课堂精练》中找几道相应的题目。课本 P90第 4 题:已知:如图,在Rt△ABC中,AB=AC,∠DAE=45° .求证:( 1)△ABE∽△ACD;(2)BC2=2BE×CDEDCAB例:在 Rt△ABC中,∠ C为直角, CD⊥AB于点 D,BC=3,AB=5,写出其中的一对相似三角形 _______________;并写出它的面积比(四)一线三等角模型:以等腰三角形(等腰梯形)或者等边三角形为背景包括“三垂直”模型:例 1:(2013· 天津 ) 如图所示,在边长为 9 的正三角形 ABC 中,BD=3,∠ADE=60° ,则 AE 的长为例 1 图例 2 图例 2:如图,等边△ ABC 中,边长为 6,D 是 BC 上动点,∠ EDF=60°(1)求证:△ BDE∽△CFD(2)当 BD=1,FC=3 时,求 BE 例 3:在△ABC 中,5ACAB,8BC,点 P 、Q 分别在射线 CB 、AC 上(点 P 不与点 C 、点 B 重合),且保持ABCAPQ. ①若点 P 在线段 CB 上(如图),且6BP,求线段 CQ 的长;②若xBP,yCQ,求 ...