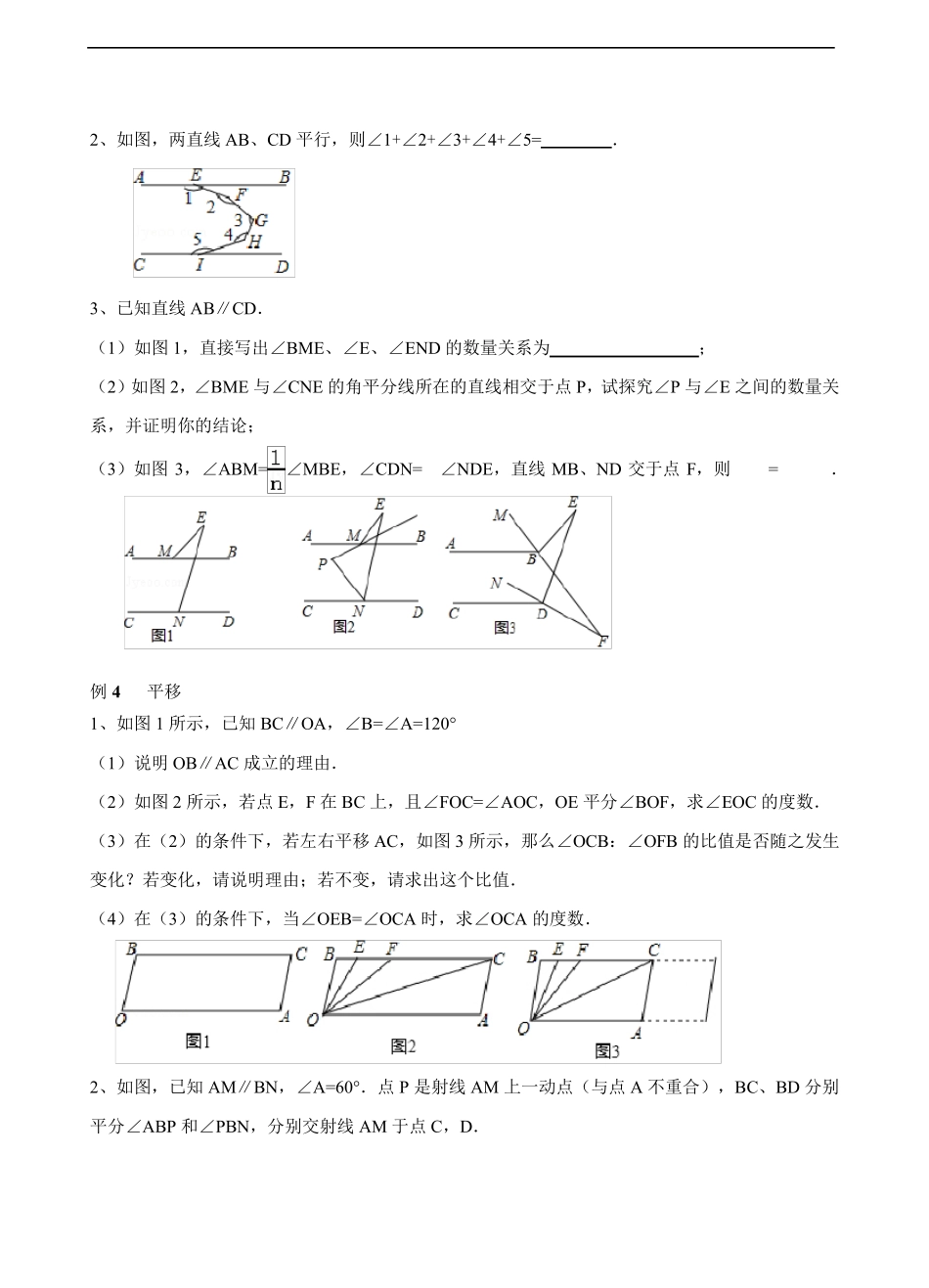
平行线 例1 翻折 1、如图,把一张长方形纸带沿着直线GF 折叠,∠CGF=30°,则∠1 的度数是 . 2、如图,生活中将一个宽度相等的纸条按图所示折叠一下,如果∠2=100°,那么∠1 的度数为 . 例2 旋转 1、将一副直角三角尺 ABC 和 CDE 按如图方式放置,其中直角顶点 C 重合,∠D=45°,∠A=30°.将三角形CDE绕点C旋转,若DE∥BC,则直线AB与直线CE的较大的夹角∠1的大小为 度. 例3 平行线的性质 1、已知,直线AB∥DC,点 P 为平面上一点,连接 AP 与 CP. (1)如图1,点 P 在直线AB、CD 之间,当∠BAP=60°,∠DCP=20°时,求∠APC. (2)如图2,点 P 在直线AB、CD 之间,∠BAP 与∠DCP 的角平分线相交于点 K,写出∠AKC 与∠APC 之间的数量关系,并说明理由. (3)如图3,点 P 落在 CD 外,∠BAP 与∠DCP 的角平分线相交于点 K,∠AKC 与∠APC 有何数量关系?并说明理由. 1AEDBC 2、如图,两直线AB、CD 平行,则∠1+∠2+∠3+∠4+∠5= . 3、已知直线AB∥CD. (1)如图1,直接写出∠BME、∠E、∠END 的数量关系为 ; (2)如图2,∠BME 与∠CNE 的角平分线所在的直线相交于点 P,试探究∠P 与∠E 之间的数量关系,并证明你的结论; (3)如图3,∠ABM=∠MBE,∠CDN=∠NDE,直线MB、ND 交于点 F,则= . 例 4 平移 1、如图1 所示,已知 BC∥OA,∠B=∠A=120° (1)说明 OB∥AC 成立的理由. (2)如图2 所示,若点 E,F 在 BC 上,且∠FOC=∠AOC,OE 平分∠BOF,求∠EOC 的度数. (3)在(2)的条件下,若左右平移 AC,如图3 所示,那么∠OCB:∠OFB 的比值是否随之发生变化?若变化,请说明理由;若不变,请求出这个比值. (4)在(3)的条件下,当∠OEB=∠OCA 时,求∠OCA 的度数. 2、如图,已知 AM∥BN,∠A=60°.点 P 是射线AM 上一动点(与点 A 不重合),BC、BD 分别平分∠ABP 和∠PBN,分别交射线AM 于点 C,D. (1)求∠CBD 的度数; (2)当点P 运动时,∠APB 与∠ADB 之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律. (3)当点P 运动到使∠ACB=∠ABD 时,∠ABC 的度数是 . 例5 作图—应用 1、(1)如图1,一个牧童从 P 点出发,赶着羊群去河边喝水,则应当怎样选择饮水路线,才能使羊群走的路程最短?请在图中画出最短路线. (2)如图2...