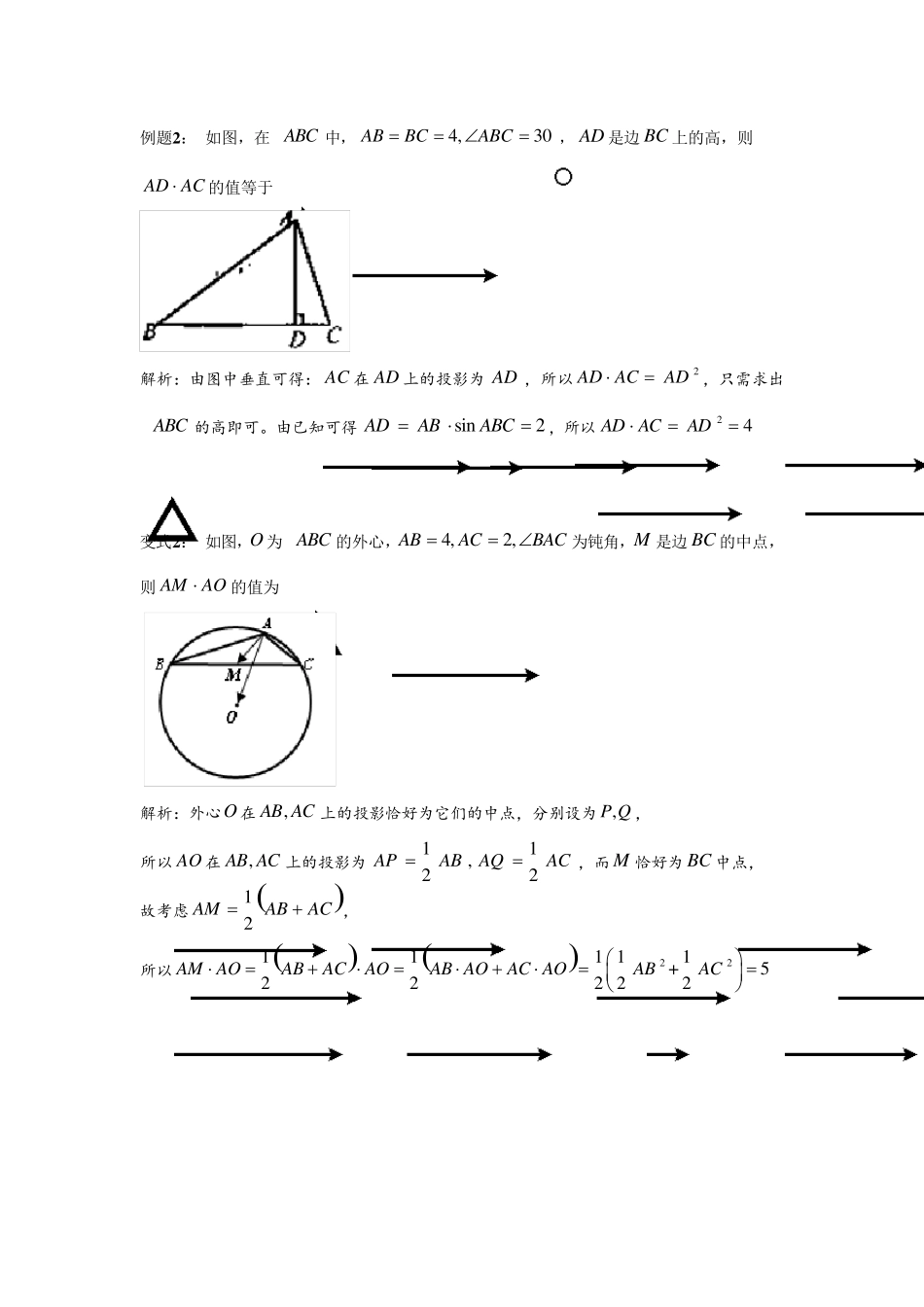
平 面 向 量 的 投 影 问 题 数量积投影定义的适用范围:作为数量积的几何定义,通常适用于处理几何图形中的向量问题。 (1)图形中出现与所求数量积相关的垂直条件,尤其是垂足确定的情况下(此时便于确定投影),例如:直角三角形,菱形对角线,三角形的外心(外心到三边投影为三边中点) (2)从模长角度出发,在求数量积的范围中,如果所求数量积中的向量中有一个模长是定值,则可以考虑利用投影,从而将问题转化为寻找投影最大最小的问题 1. 定 值 问 题 例题1: 已知向量满足,且,则在方向上的投影为 解析:考虑b 在a 上的投影为a bb,所以只需求出a b即可。由 aab 可得:20aabaa b,所以 9a b 。进而933223a bb 变式1: 两 个 半 径 分 别 为12,r r 的圆,M N , 公 共 弦 AB 长 为3 ,如 图所 示 ,则AM ABAN AB __________. 分析:AB 为两个圆的公共弦,从而圆心,M N 到弦 AB 的投影为AB 的中点,进而,AM AN在AB 上的投影能够确定,所以考虑计算 AM AB和 AN AB时可利用向量的投影定义。 解析:取 AB 中点T ,连结,MT NT ,由圆的性质可得:,MTAB NTAB 21922AM ABATABAB 21922AN ABATABAB 9AM ABAN AB ,a b3 ,23abaabba例题2: 如图,在ABC 中,4,30ABBCABC,AD 是边BC 上的高,则AD AC的值等于 解析:由图中垂直可得:AC 在AD 上的投影为AD ,所以2AD ACAD,只需求出ABC 的高即可。由已知可得sin2ADABABC,所以24AD ACAD 变式2: 如图,O 为 ABC 的外心,4,2,ABACBAC为钝角,M 是边BC 的中点,则 AMAO的值为 解析:外心O 在,AB AC 上的投影恰好为它们的中点,分别设为,P Q , 所以AO 在,AB AC 上的投影为 11,22APABAQAC,而 M 恰好为BC 中点, 故考虑12AMABAC, 所以22111 11+5222 22AM AOABACAOAB AOAC AOABAC 2. 范 围 问 题 例题3: 若过点 1,1P的直线l 与 22:4O xy相交于,A B 两点,则OA OB的取值范围是_______ 解析:本题中因为,OA OB 位置不断变化,所以不易用数量积定义求解,可考虑利用投影,即过B 作直线OA 的垂线, 垂足为D ,通过旋转AB 可发现,当OBO...