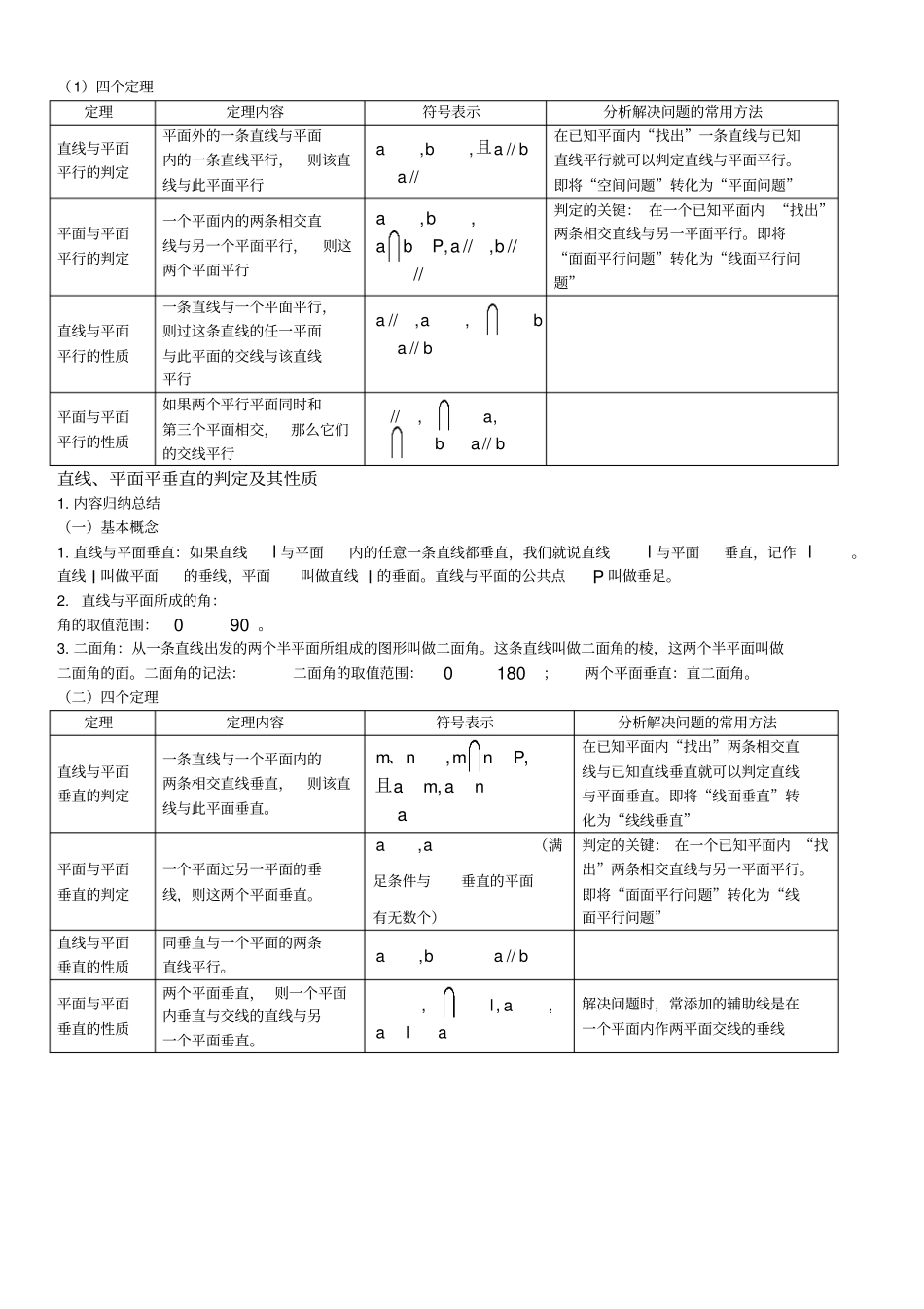
《空间中点、直线、平面之间的位置关系》知识点总结1. 内容归纳总结(1)四个公理公理 1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。符号语言:,,,Al BlABl且。公理 2:过不在一条直线上的三点,有且只有一个平面。三个推论:①经过一条直线和这条直线外一点,有且只有一个平面② 经过两条相交直线,有且只有一个平面③ 经过两条平行直线,有且只有一个平面它给出了确定一个平面的依据。公理 3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线(两个平面的交线)。符号语言:,,PPl Pl且。公理 4:(平行线的传递性)平行与同一直线的两条直线互相平行。符号语言:// ,////alblab且。(2)空间中直线与直线之间的位置关系1. 概念异面直线及夹角:把不在任何一个平面内的两条直线叫做异面直线。已知两条异面直线,a b ,经过空间任意一点O 作直线//,//aa bb ,我们把 a 与 b 所成的角(或直角)叫异面直线,a b 所成的夹角。 (易知:夹角范围090 )定理:空间中如果一个角的两边分别与另一个角的两边分别平行,那么这两个角相等或互补。(注意:会画两个角互补的图形)2. 位置关系:相交直线:同一平面内,有且只有一个公共点;共面直线平行直线:同一平面内,没有公共点;异面直线:不同在任何一个平面内,没有公共点(3)空间中直线与平面之间的位置关系直线与平面的位置关系有三种:/ /llAl直线在平面内()有无数个公共点直线与平面相交()有且只有一个公共点直线在平面外直线与平面平行()没有公共点(4)空间中平面与平面之间的位置关系平面与平面之间的位置关系有两种:/ /l两个平面平行()没有公共点两个平面相交()有一条公共直线直线、平面平行的判定及其性质1. 内容归纳总结(1)四个定理定理定理内容符号表示分析解决问题的常用方法直线与平面平行的判定平面外的一条直线与平面内的一条直线平行,则该直线与此平面平行,,////ababa且在已知平面内“找出”一条直线与已知直线平行就可以判定直线与平面平行。即将“空间问题”转化为“平面问题”平面与平面平行的判定一个平面内的两条相交直线与另一个平面平行,则这两个平面平行,,,//, ////ababP ab判定的关键: 在一个已知平面内 “找出”两条相交直线与另一平面平行。即将“面面平行问题”转化为“线面平行问题”直线与平面平行的性质一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直...