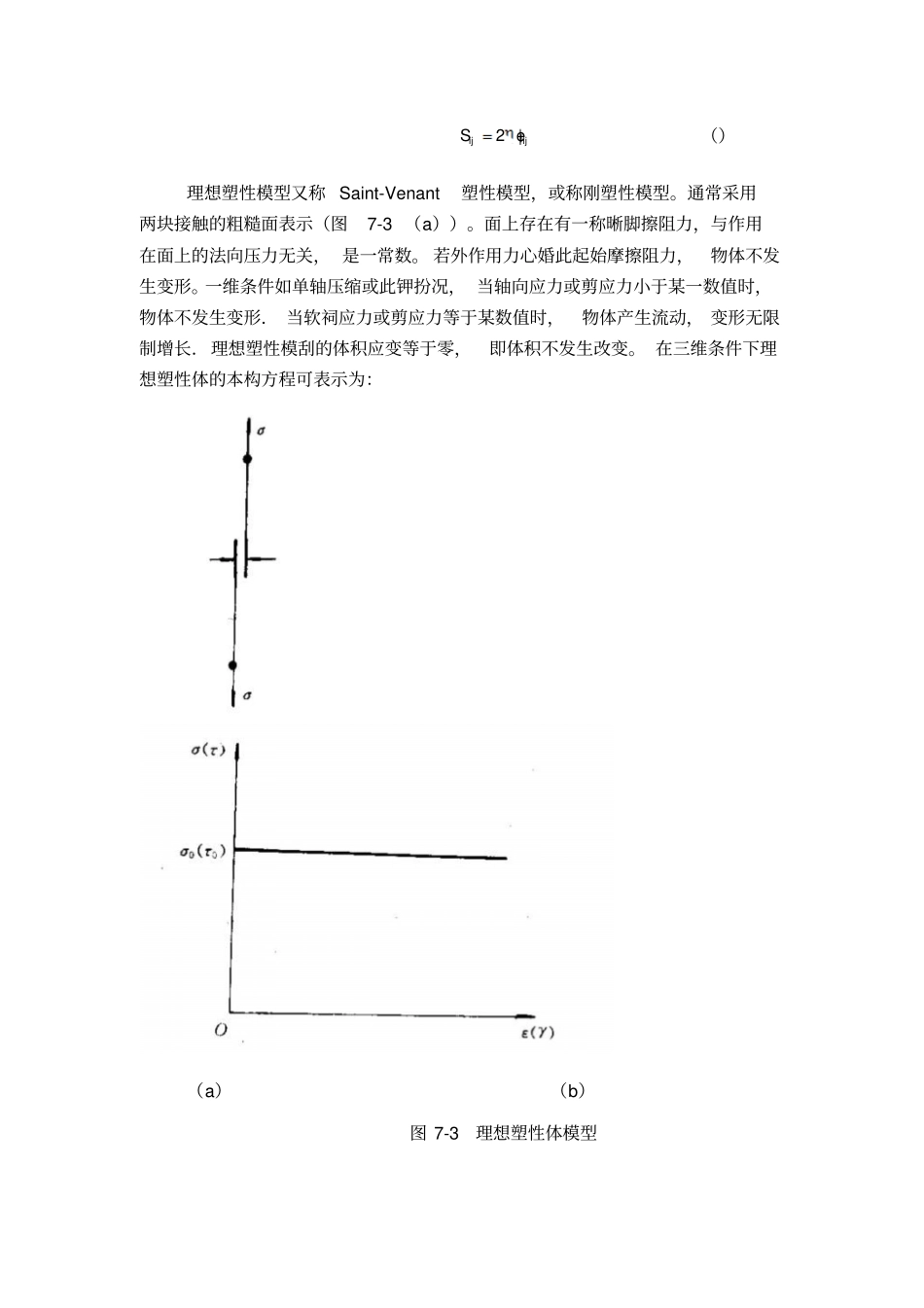
第七章 粘弹塑性模型的基本概念7 . 1 引言为了描述土体应力一应变关系受时间的影响,需要采用与时间有关的类模型(如粘弹胜模酬、粘塑性模型,粘弹塑隆模型)来描述土的性状。弹性、塑性和粘性是连续介质的三种基本性质,各在定条件F 独自反映材料本构关系的一个方面的特性。理想弹性模型、 理想塑胜模型 (或称刚塑性模型)和理想粘性模型是反映这三种性质的理想模型,通常称为简单模型。 实际工程材料的本构关系可以用这些简单模型的各种组合来构成。理想弹性模型又称虎克弹性模型,通常用理想弹簧表示(图7-1( a ))。其本构方程为虎克定律。一维条件下,如单轴压缩和纯剪清况下,表达式分别为:E(7.1.1 )G(7.1.2 )式中 E —— 弹性模量、G——剪切模量。剪切模量与弹性模量和泊松比的关系如下式所示:2 1EG(7.1.3 )式中——泊松比。三维条件下本构方程可表示为下述形式:mK(7.1.4 )式中 K ——体积弹性模量。(a)(b)图 7-1 理想弹性模型体积弹性模量与弹性模量和泊松比的关系如下式所示:3 12EK(7.1.6 )理想粘性模型又称牛顿粘滞体模型。通常用一粘壶 (或称阻尼器) 表示(图7-2 ( a ) )。粘壶内充满粘滞液体和一个可移动的活塞。活塞在粘滞液体中的移动速度与所受阻力成正比关系, 反映了粘性介质内一点的应力与该点处应变速率成正比例关系的性质。一维条件如单轴压缩或纯剪情况下,表达式分别为:(7.1.7 )(7.1.8 )式中、——粘滞系数。由上两式可以看出, 从数学表达的形式上与理想弹性体单轴压缩和纯剪时的本构方程相类似。与理想弹性体的方程相对应,类似式7.1.3 ,存在下述关系:*2 1(7.1.9 )式中* ——粘性应变速率的横向比值。(a)(b)图 7-2 理想粘性模型理想粘性体的体积变化与形状变化速率无关,即不具有体积粘性。因此,* 应等于 0.5 。于是式 7.1.9 成为:3()这与弹性不可压缩时的E=3G相对应。在三维条件下理想粘性体本构方程可表示为:2ijijSe()理想塑性模型又称 Saint-Venant 塑性模型,或称刚塑性模型。通常采用两块接触的粗糙面表示(图7-3 (a))。面上存在有一称晰脚擦阻力,与作用在面上的法向压力无关, 是一常数。 若外作用力心婚此起始摩擦阻力,物体不发生变形。一维条件如单轴压缩或此钾扮况, 当轴向应力或剪应力小于某一数值时,物体不发生变形. 当软祠应力或剪应力等于某数值时,物体产生流动, 变形无限制增长.理想塑性模刮...