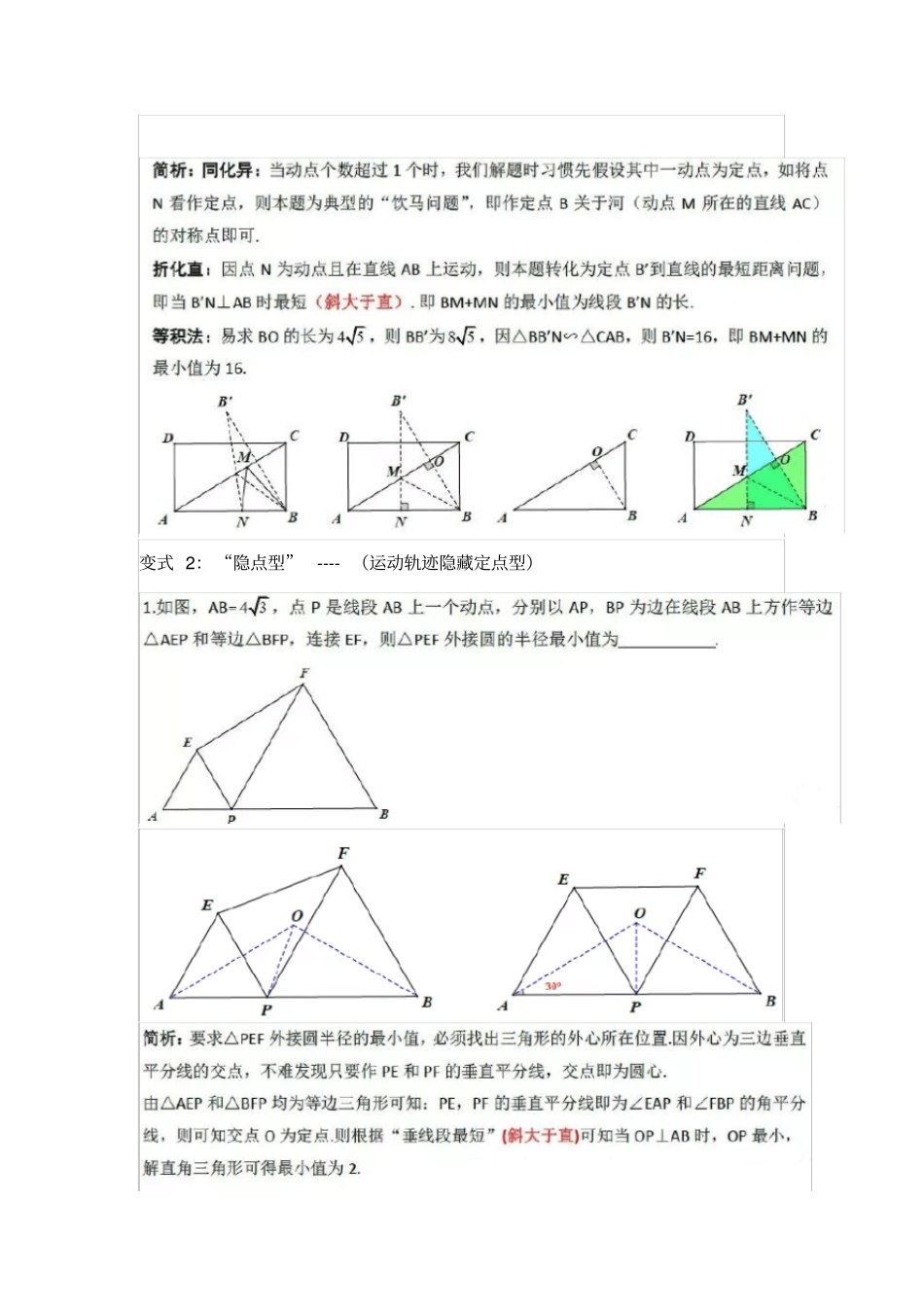
中考数学压轴题突破线段最值探索(斜大于直思想)一、相关知识点: 1、点到直线的距离:( 1). 通常,我们把直线外一点到这条直线的垂线段的长度叫做点到直线的距离;( 2). 经过探究我们得到一个事实:直线外一点与直线上各点连接的所有线段中,垂线段最短. 即我们今天所要讲的内容“斜大于直”问题。“斜大于直”问题在中考线段最值中考察较为广泛,即点到线的最短距离问题,常见的有: 1. 单线段的最值; 2. 线段和的最小;3. 系数不为1 的线段和的最值(胡不归问题).二、例题精选基 本 模 型 : 点P到 直 线MN的 最 短 距 离 为 线 段PA的 长 .变式 1: “隐点型”---- (对称隐藏定点型)变式 2: “隐点型”---- (运动轨迹隐藏定点型)反思: ①本题的关键在于确定△ PEF 的外心, 利用等边三角形的特殊性将垂直平分线的交点转化为角平分线的交点,寻找到外心.②发现外心为一定点,则转化为求定点到直线的最短距离问题,即垂线段最短(斜大于直).变式 3: “隐点型”---- (运动轨迹隐藏定点型)反思: ①看起来是“点到点”实质为“点到线”.②本题关键在于发现△ABQ为固定的直角三角形.③由矩形对角线相等将MN转化为PQ,则转化为求定点Q 到直线的最短距离问题,即垂线段最短(斜大于直). 变式 4: “隐线型”---- (运动隐藏直线轨迹型)变式 5 :“隐线型”---- (运动隐藏直线轨迹型)反思: ①找到点T, N 的轨迹是本题的首要任务,直线型轨迹的寻找常用方法都是定点定角寻找,即找到过某一定点的定角,点的轨迹即为直线. 本题中∠PAN,∠ TAC均为定值,又经过定点A,则轨迹不难发现为是直线.②再利用“斜大于直”思想,迅速解答此题. 变式 6: “隐线型”---- (运动隐藏直线轨迹型)变式 7: “隐线型”---- (运动隐藏直线轨迹型----胡不归问题型)总结:由上述题组可以发现“斜大于直”问题考察题型较为广泛,可以是单一线段最值,也可是多条线段最值,还能是含系数的线段和的最值问题,不管是其中那种类型,都可以利用转化思想对问题进行巧妙处理。①单线段的最值常见于直接型的点到直线距离问题,当然也可以将定点隐藏“隐点” 或将动点形成的直线型轨迹隐藏“隐线” ,题目难度就会大大加深。②多线段和的最值始终遵循“同化异,折化直”的解题思路来进行,如遇线段带系数,思考能否运用三角函数将系数转化。不管是 “隐点” 还是 “隐线” 最终都会转化为点到线的距离问题,即始终抓住 “斜大于直”思想找出最短距离即可。