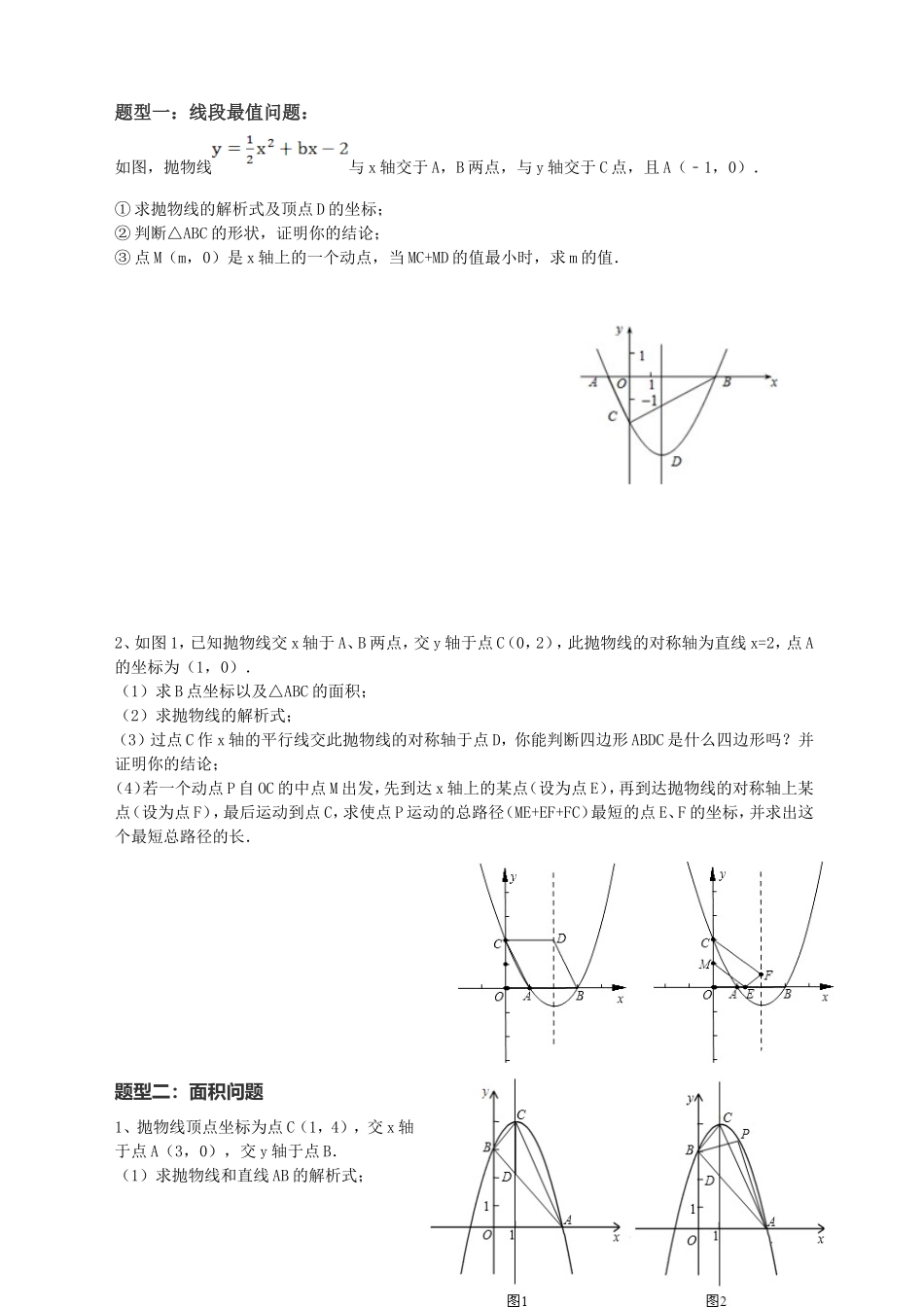
题型一:线段最值问题: 如图,抛物线与 x 轴交于 A,B 两点,与 y 轴交于 C 点,且 A(﹣1,0).① 求抛物线的解析式及顶点 D 的坐标;② 判断△ABC 的形状,证明你的结论;③ 点 M(m,0)是 x 轴上的一个动点,当 MC+MD 的值最小时,求 m 的值.2、如图 1,已知抛物线交 x 轴于 A、B 两点,交 y 轴于点 C(0,2),此抛物线的对称轴为直线 x=2,点 A的坐标为(1,0).(1)求 B 点坐标以及△ABC 的面积;(2)求抛物线的解析式;(3)过点 C 作 x 轴的平行线交此抛物线的对称轴于点 D,你能判断四边形 ABDC 是什么四边形吗?并证明你的结论;(4)若一个动点 P 自 OC 的中点 M 出发,先到达 x 轴上的某点(设为点 E),再到达抛物线的对称轴上某点(设为点 F),最后运动到点 C,求使点 P 运动的总路径(ME+EF+FC)最短的点 E、F 的坐标,并求出这个最短总路径的长.题型二:面积问题1、抛物线顶点坐标为点 C(1,4),交 x 轴于点 A(3,0),交 y 轴于点 B.(1)求抛物线和直线 AB 的解析式;(2)连结 CA,CB,对称轴 x=1 与线段 AB 交于点 D,求△CAB 的铅垂高 CD 及 S △CAB ;(3)如图 2,点 P 是抛物线(在第一象限内)上的一个动点,连结 PA,PB,是否存在一点 P,使 S △PAB = S△CAB ?若存在,求出 P 点的坐标;若不存在,请说明理由.2、如图,抛物线 y=ax2+bx+4 与 x 轴的两个交点分别为 A(-4,0)、B(2,0),与 y 轴交于点 C,顶点为 D. E(1,2)为线段 BC 的中点,BC 的垂直平分线与 x 轴、y 轴分别交于 F、G.(1)求抛物线的函数解析式,并写出顶点 D 的坐标;(2)在直线 EF 上求一点 H,使△CDH 的周长最小,并求出最小周长;(3)若点 K 在 x 轴上方的抛物线上运动,当 K 运动到什么位置时,△EFK 的面积最大?并求出最大面积.题型三:等腰三角形问题1、如图,点 A 在 x 轴上,OA=4,将线段 OA 绕点 O 顺时针旋转 120°至 OB 的位置.(1)求点 B 的坐标; (2)求经过点 A、O、B 的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点 P,使得以点 P、O、B 为顶点的三角形是等腰三角形?若存在,求点 P 的坐标;若不存在,说明理由.如图,直线 y=3x+3 交 x 轴于 A 点,交 y 轴于 B 点,过 A、B 两点的抛物线交 x 轴于另一点C(3,0).1、...