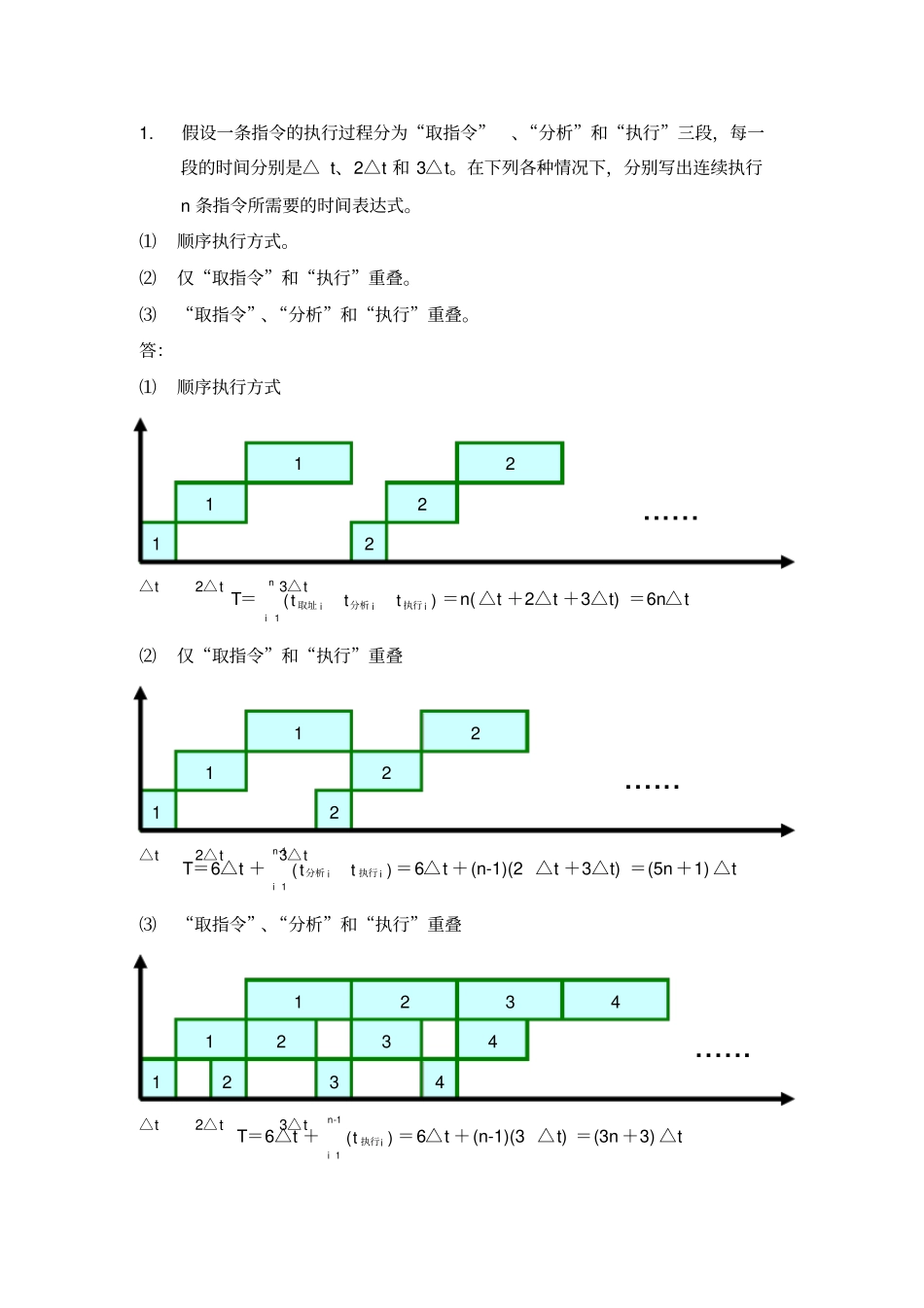
1. 假设一条指令的执行过程分为“取指令”、“分析”和“执行”三段,每一段的时间分别是△ t、2△t 和 3△t。在下列各种情况下,分别写出连续执行n 条指令所需要的时间表达式。⑴顺序执行方式。⑵仅“取指令”和“执行”重叠。⑶“取指令”、“分析”和“执行”重叠。答:⑴顺序执行方式1 2 ......1 2 1 2 T=n1iiii)ttt(执行分析取址=n( △t +2△t +3△t) =6n△t ⑵仅“取指令”和“执行”重叠1 2 ......1 2 1 2 T=6△t +1-n1iii)tt(执行分析=6△t +(n-1)(2 △t +3△t) =(5n +1) △t ⑶“取指令”、“分析”和“执行”重叠1 2 3 4 ......1 2 3 4 1 2 3 4 T=6△t +1-n1ii )t(执行=6△t +(n-1)(3 △t) =(3n +3) △t△t2△t3△t△t2△t3△t△t2△t3△t2. 一条线性流水线有4 个功能段组成,每个功能段的延迟时间都相等,都为△t。开始 5 个任务,每间隔一个△ t 向流水线输入一个任务,然后停顿2个△ t,如此重复。求流水线的实际吞吐率、加速比和效率。答:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ...1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 我们可以看出,在( 7n+1)Δ t 的时间内,可以输出5n 个结果,如果指令的序列足够长( n→∞),并且指令间不存在相关,那么,吞吐率可以认为满足:加速比为:从上面的时空图很容易看出,效率为:3. 用一条 5 个功能段的浮点加法器流水线计算101iiAF。每个功能段的延迟时间均相等,流水线的输出端与输入端之间有直接数据通路,而且设置有足够的缓冲寄存器。要求用尽可能短的时间完成计算,画出流水线时空图,计算流水线的实际吞吐率、加速比和效率。答:首先需要考虑的是“ 10 个数的和最少需要做几次加法?” ,我们可以发现,加法的次数是不能减少的:9 次;于是我们要尽可能快的完成任务,就只有考虑如何让流水线尽可能充满, 这需要消除前后指令之间的相关。由于加法满足交换律和结合律, 我们可以调整运算次序如以下的指令序列,我们把中间结果寄存器称为 R,源操作数寄存器称为A,最后结果寄存器称为F,并假设源操作数已经在寄存器中,则指令如下:I1:R1←A1+A2 I2:R2←A3+A4...