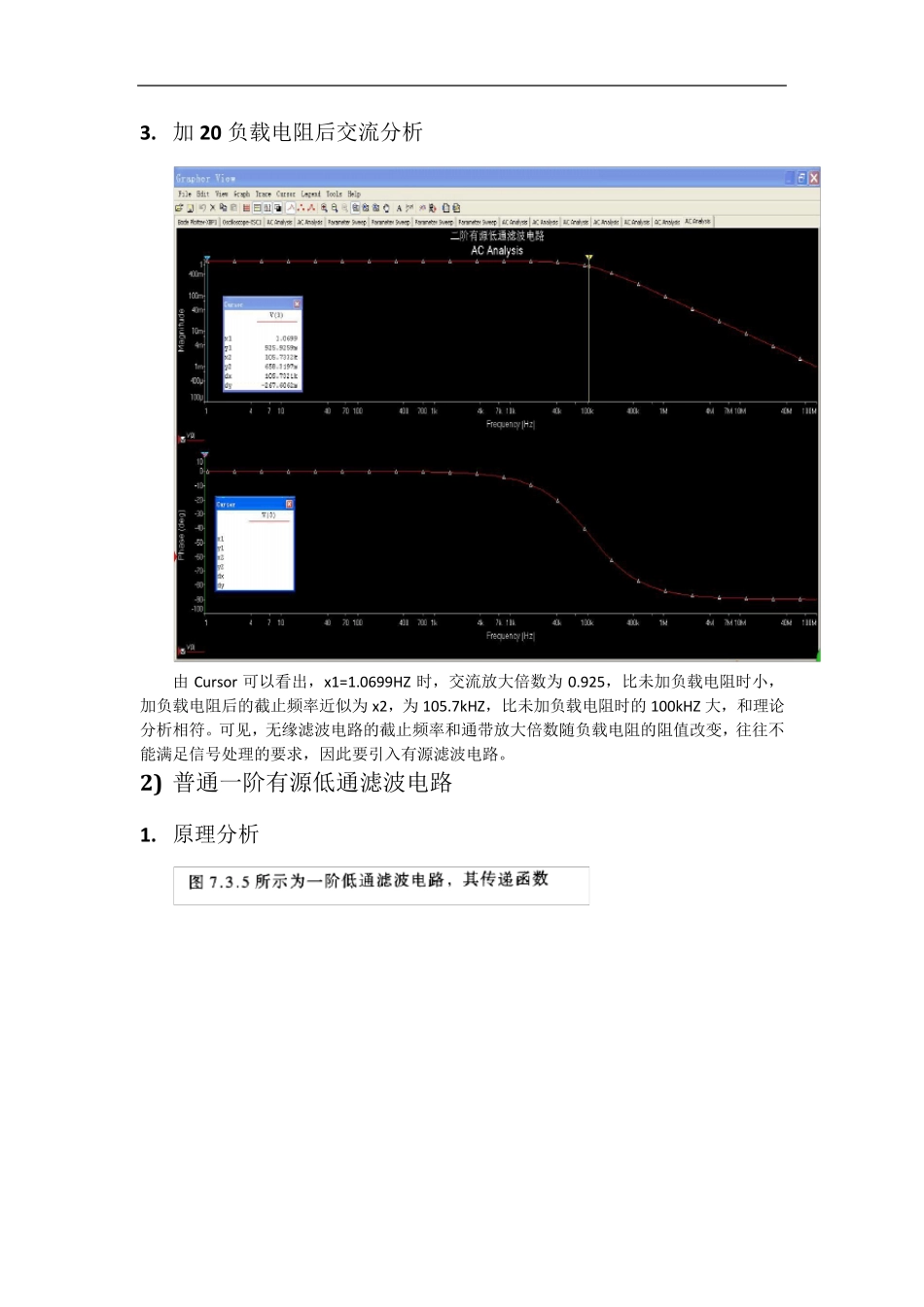
有源低通滤波电路 1 ) 一阶无源低通滤波电路 1 . 理论分析 2 . 交流分析 从Cursor 栏可以看出,f=1.0MHz 时,y1=98.4415,f=100MHZ 时,y2=990.9547,频率相差一百倍,交流放大倍数只比也近似为100 倍,和理论分析吻合。 3. 加20 负载电阻后交流分析 由Cursor 可以看出,x1=1.0699HZ 时,交流放大倍数为0.925,比未加负载电阻时小,加负载电阻后的截止频率近似为x2,为105.7kHZ,比未加负载电阻时的100kHZ 大,和理论分析相符。可见,无缘滤波电路的截止频率和通带放大倍数随负载电阻的阻值改变,往往不能满足信号处理的要求,因此要引入有源滤波电路。 2 ) 普通一阶有源低通滤波电路 1. 原理分析 2 . 仿真图 3. 交流分析 和原理分析的结果相同,当f=f 0 =12πRC =12∗3.14∗1.6∗103∗1∗10− 9 = 99.5kHZ ,Au =0.7Au f=0.7*2=1.4,当f>>f0 时,f 每增大十倍,交流放大倍数是原来的十分之一。 3 ) 普通二阶有源低通滤波器 1. 原理分析 由理论分析可知,在一阶低通滤波的基础上加一个低通滤波,变成了二阶低通滤波电路。二阶低通滤波电路幅频特性的最大衰减速率是 40db/dec,是一阶低通滤波电路的两倍,但f=0.37fo 时,Au=0.707Auf,即在f0 附近的有用信号会得到较大幅度的衰减,因此有必要加入正反馈,使电路的滤波性能得到提升。 2. 仿真图 3. 交流分析 由Cursor 栏可知,当f=0.37fo=37kHZ 时,Au=0.7Auf=1.4,和理论分析吻合。 4) 压控电源二阶低通滤波 1. 理论分析 由理论分析可知,当f=f0 时,Au/Aup=Q,在f=f0 时的电压放大倍数和Q 值有关,Q 值大于1 时,Au 在f=f0 处大于Aup。Q 值越大,f=f0 处,Au/Aup 越大。 2. 仿真图 3. 交流分析 根据交流分析可知,当f=f0=100kHZ 时。Au=Aup=2,和理论分析吻合。 4. Q 值分析 从理论分析可知,不同的Q 值在f=f0 处的幅值曲线的陡度不一样,取R4 分别等于0Ω,6200Ω,9300Ω,分别对应 Q 值为 0.5,2,仿真波形如下图所示 从仿真图的Cursor 栏可以看出,f=f0=100kHZ,R4=6200Ω时,y1=1.9854≈2,和理论相符,R4=0Ω时,y1=496.628m≈0.5,为 R4=6200 欧姆的1/4,和 Q 值的倍数相同,与理论分析吻合,R4=9300 时,y1=4.8547≈5,是 R4=6200 欧姆的2.5 倍,和 Q 值的倍数相同,与理论分析吻合。