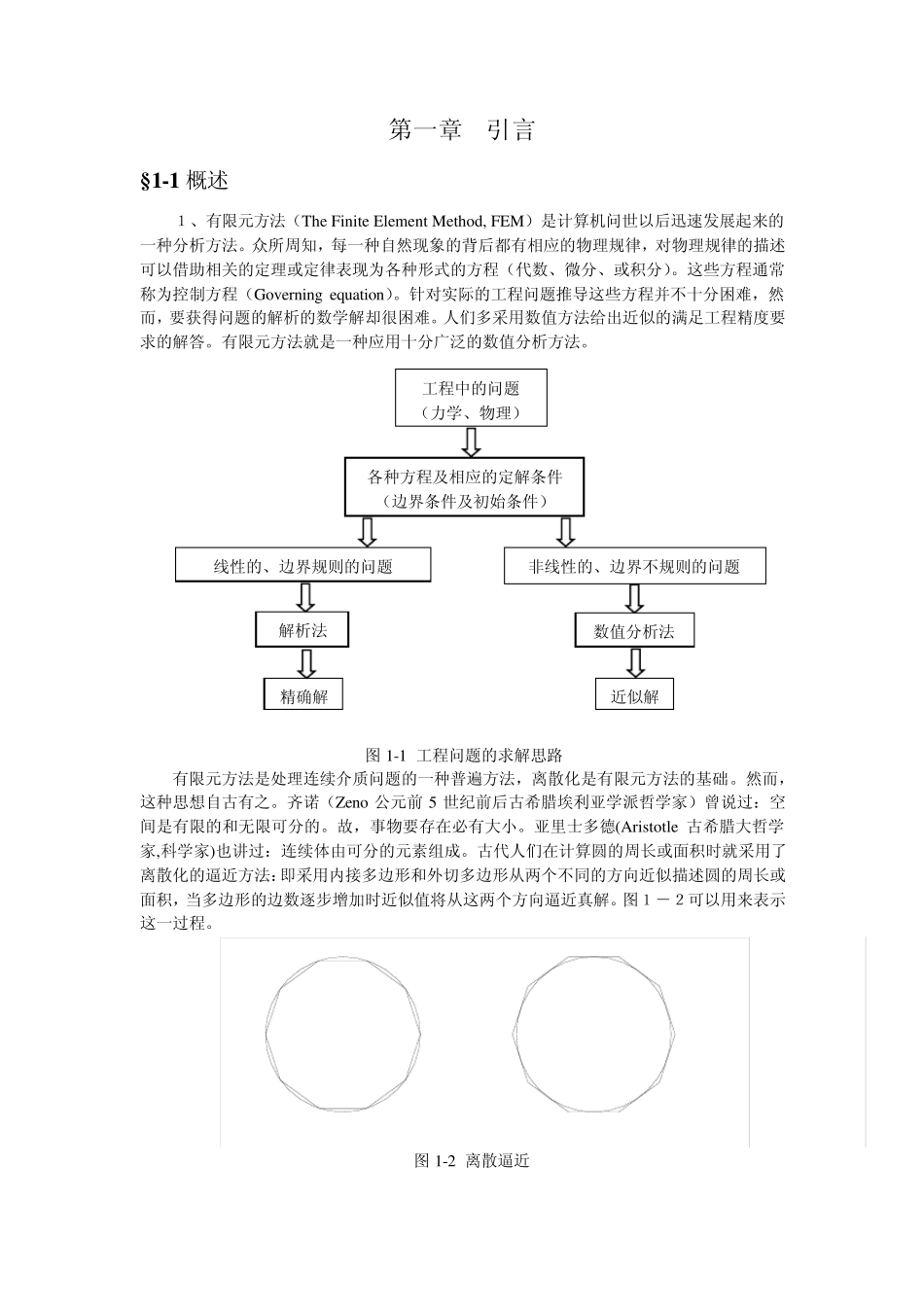
第一章 引言 § 1-1 概述 1、有限元方法(The Finite Element Method, FEM)是计算机问世以后迅速发展起来的一种分析方法。众所周知,每一种自然现象的背后都有相应的物理规律,对物理规律的描述可以借助相关的定理或定律表现为各种形式的方程(代数、微分、或积分)。这些方程通常称为控制方程(Gov erning equ ation)。针对实际的工程问题推导这些方程并不十分困难,然而,要获得问题的解析的数学解却很困难。人们多采用数值方法给出近似的满足工程精度要求的解答。有限元方法就是一种应用十分广泛的数值分析方法。 有限元方法是处理连续介质问题的一种普遍方法,离散化是有限元方法的基础。然而,这种思想自古有之。齐诺(Zeno 公元前 5 世纪前后古希腊埃利亚学派哲学家)曾说过:空间是有限的和无限可分的。故,事物要存在必有大小。亚里士多德(Aristotle 古希腊大哲学家,科学家)也讲过:连续体由可分的元素组成。古代人们在计算圆的周长或面积时就采用了离散化的逼近方法:即采用内接多边形和外切多边形从两个不同的方向近似描述圆的周长或面积,当多边形的边数逐步增加时近似值将从这两个方向逼近真解。图1-2可以用来表示这一过程。 工程中的问题 (力学、物理)各种方程及相应的定解条件 (边界条件及初始条件) 线性的、边界规则的问题 数值分析法 精确解 近似解 非线性的、边界不规则的问题 解析法 图 1-1 工程问题的求解思路 图 1-2 离散逼近 有限单元法 有限差分法 图 1-3 有限元法与有限差分法比较 近代,这一方法首先在航空结构分析中取得了明显的效果:一种称为框架分析法(framework method)被用来分析平面弹性体(将平面弹性体描述为杆和梁的组合体)(1941,Hrenikoff);在采用三角形单元及最小势能原理研究 St.Venant 扭转问题时,分片连续函数被用来在子域中近似描述未知函数(1943, Courant)。此后,本方法在固体力学、温度场和温升应力、流体力学、流固耦合(水弹性)问题,以及航空、航天、建筑、水工、机械、核工程和生物医学等方面获得了广泛的应用。从而,促成了一个内容十分丰富的新兴分支───计算力学的出现,长期以来在力学中存在的求解手段落后于基本理论的现象得到了根本的扭转。由于拥有了强有力的分析手段,相比之下对物质世界本身(例如本构关系)的了解反而出现了一些新的薄弱环节。有限元方法的第二个关键时期出现于二十世纪六十年代中期,归功于Argyris,...