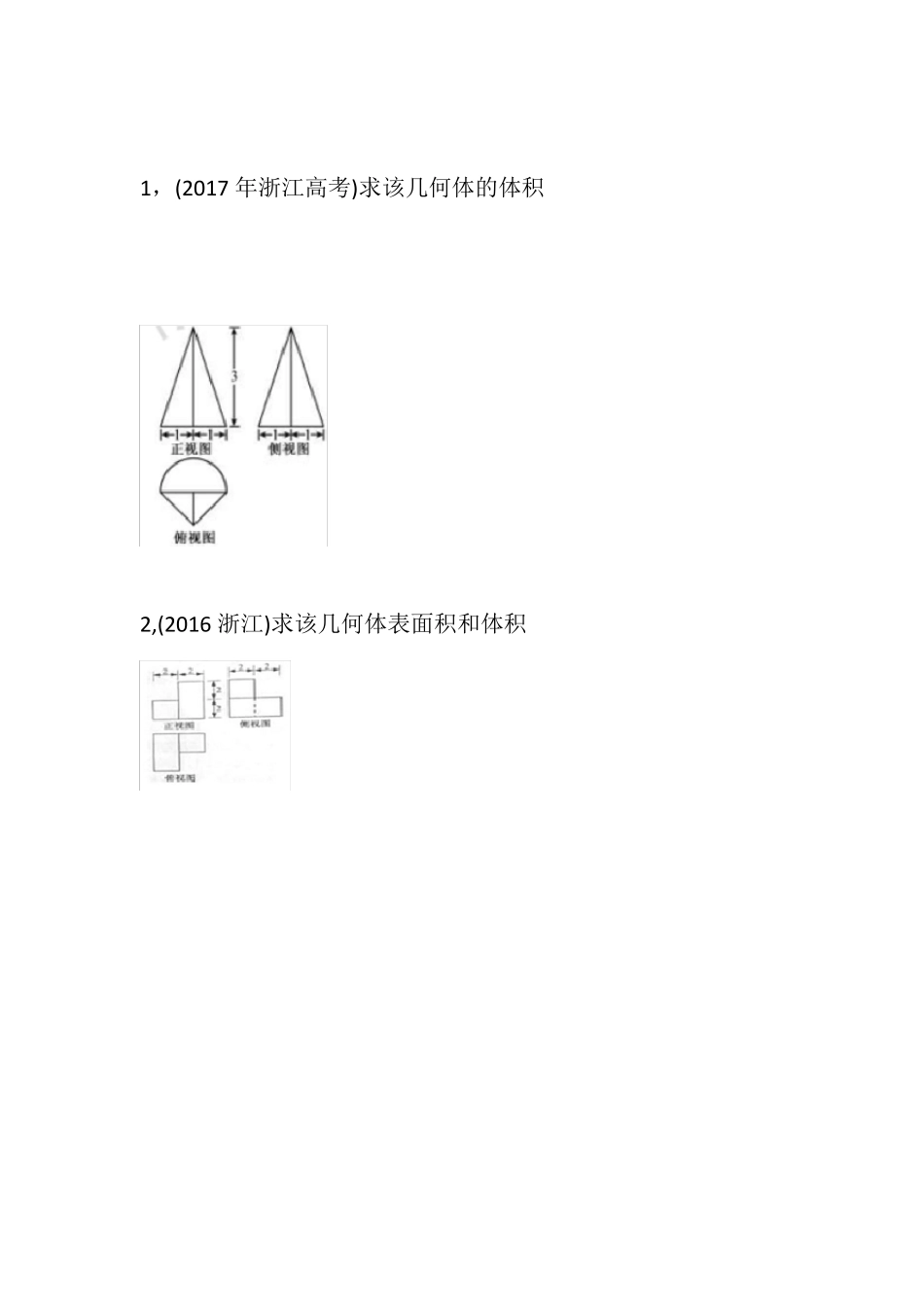
2018 年高考空间几何体三视图典型例题高三数学命题意图:主要考察几何体的三视图还原成立体图的能力,会准确求出几何体体积和表面积,考察学生的空间想象能力和计算求解能力。其中正确将三视图还原是解题的关键。浙江高考近三年来均考察三视图的体积计算,大约分值 4 分-6 分之间,这点请学生们务必重视起来。一,三视图画法坚持一下原则1,先画出一个长方体,试着根据给出的三视图画出立体图2,长对正:正视图和俯视图的长要相等3,高平齐:正视图和侧视图的高要相等4,宽相等:侧视图和俯视图的宽要相等5,实线是可以看见的部分,没有遮住6,虚线是不可以看见部分,被遮挡住7,重叠的线只画一条二,空间几何体的体积和表面积1,圆柱,体积公式:V r 2h, 侧面积 : S侧 2 rl , 底面积 :S底 2 r 21 r 2h, 侧面积 : S侧 rl , 底面积 :S底 r 2343, 球,体积公式:V r 3, 表面积 : S 4 R 232,圆锥 ,体积公式:V 4,圆台和棱台的体积公式可统一为V 1 (S SS ' S ')h(S , S '分别为上下底面的面积,h为高 )35,圆台表面积公式S台侧 (r r ')l, S表面积 (r 2 r '2 rl r 'l)(r, r '上下地面的半径, l为母线长 )1,(2017 年浙江高考)求该几何体的体积2,(2016 浙江)求该几何体表面积和体积3,(2015 浙江)求该几何体表面积和体积4,(2014 浙江)求该几何体表面积5,(2013 浙江)求该几何体的体积6,(2012 浙江)求该几何体的体积8,(2017 北京理)某四棱锥的三视图,求四棱锥最长棱的长度9,(2017 北京文)某三棱锥的三视图,求三棱锥的体积10,(2015 年安徽)求四面体的表面积11,(2015 天津)求该几何体的体积12,(2016 天津)已知四棱锥底面是平行四边形,三视图如图所示,则四棱锥的体积12,(2016 北京文)求四棱柱的体积13,(2016 北京理)求几何体的体积14,(2015 重庆)求几何体的体积