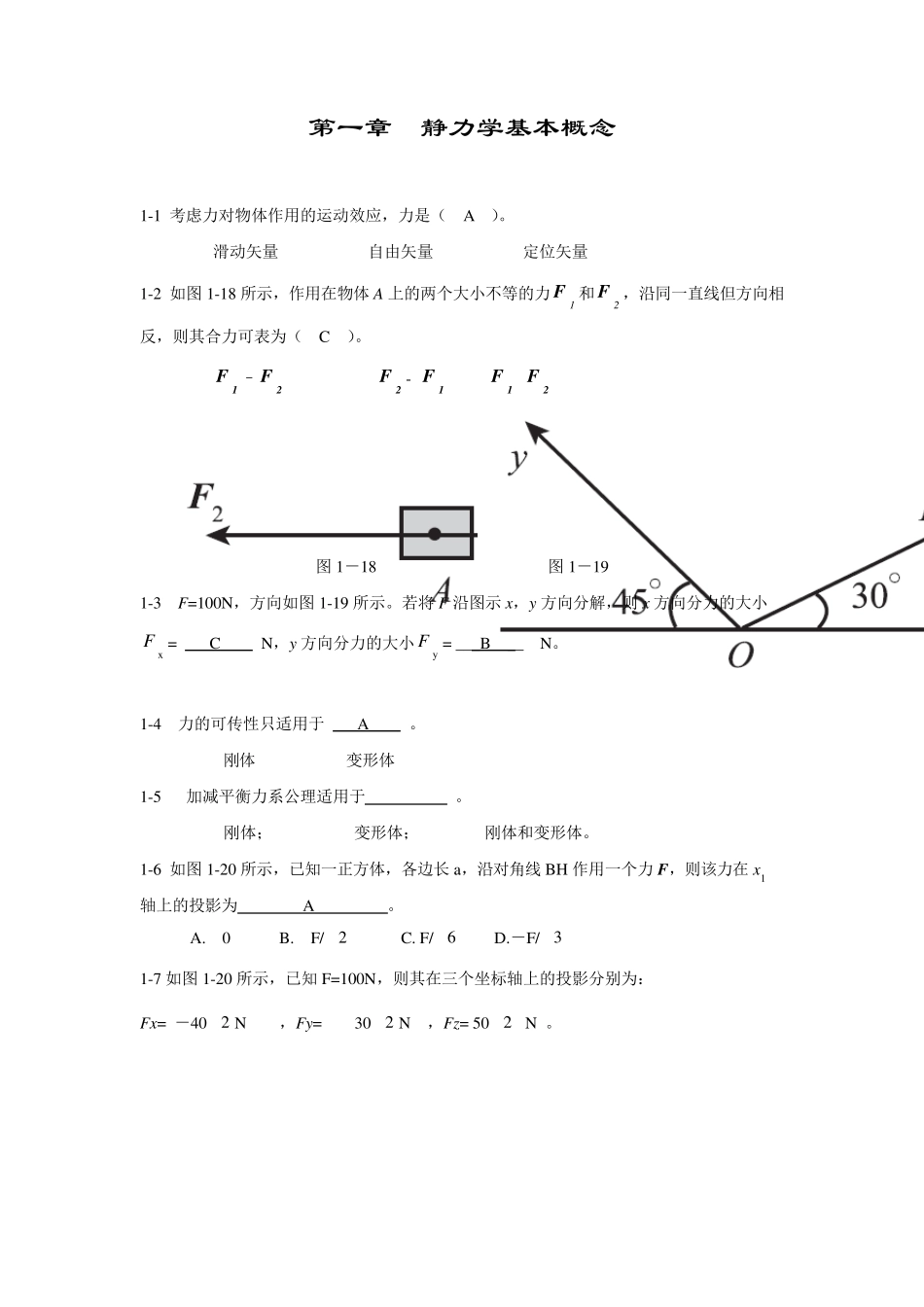
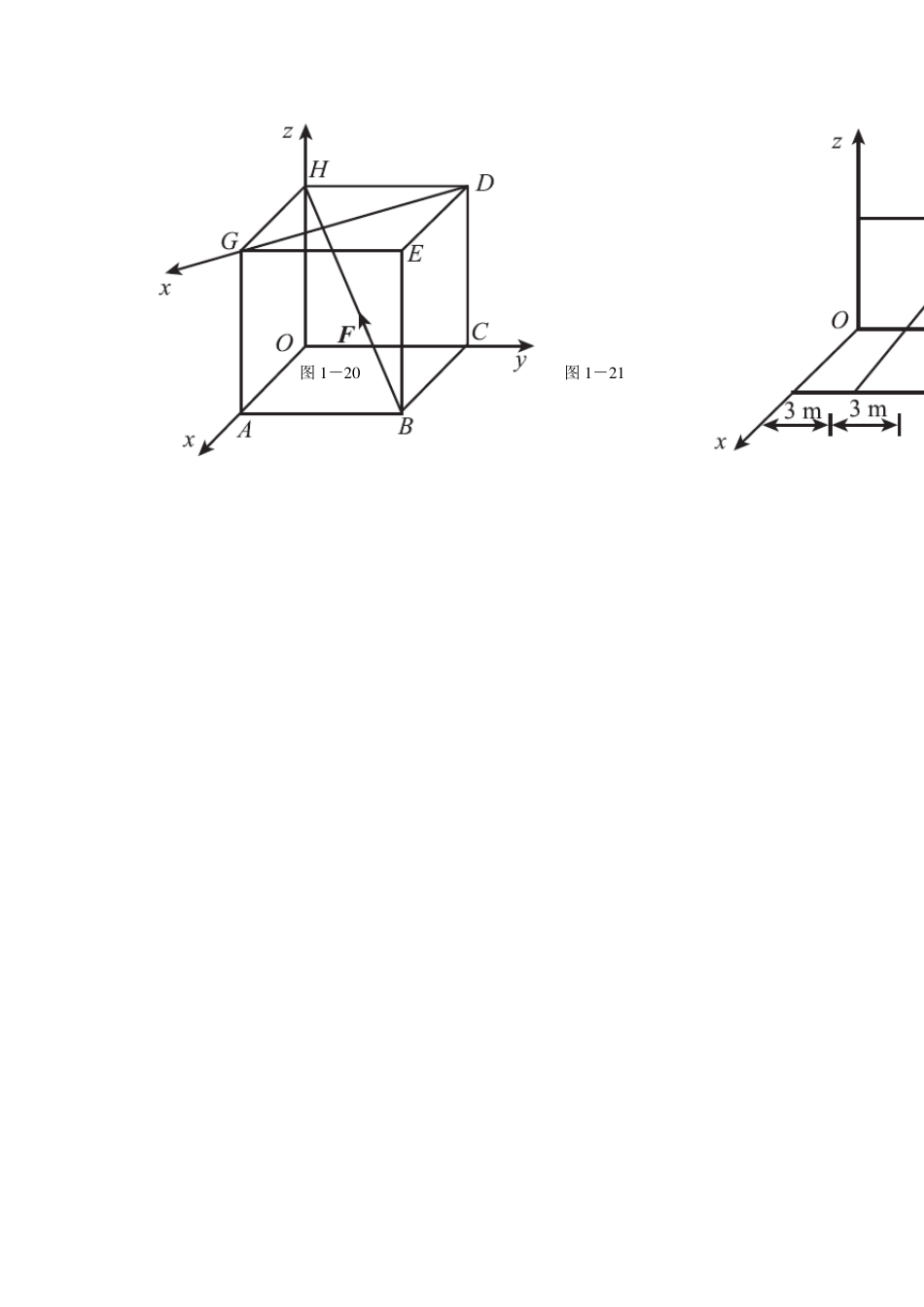
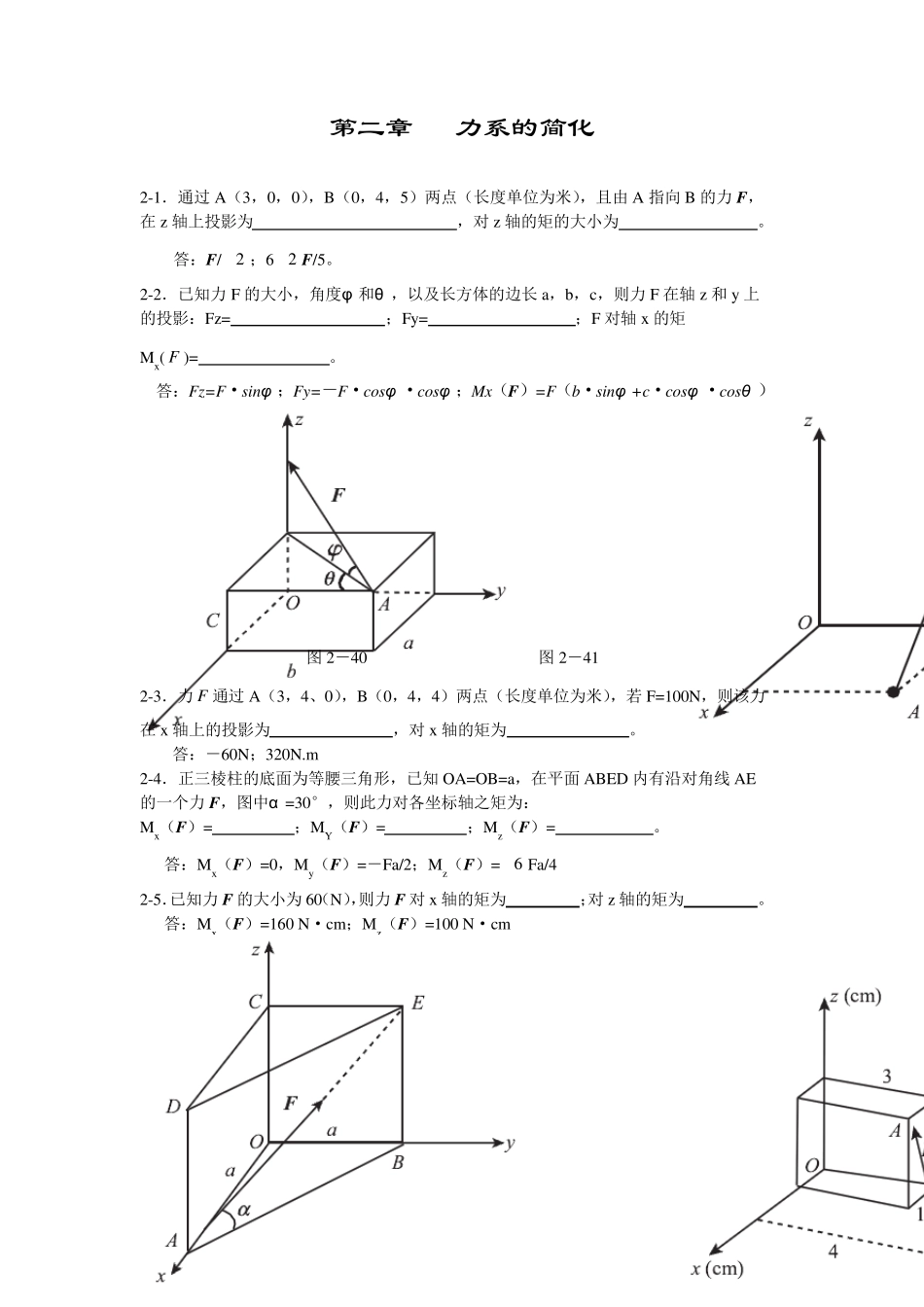
第一章 静力学基本概念 1-1 考虑力对物体作用的运动效应,力是( A )。 A.滑动矢量 B.自由矢量 C.定位矢量 1-2 如图1-18 所示,作用在物体A 上的两个大小不等的力1F和2F,沿同一直线但方向相反,则其合力可表为( C )。 A.1F–2F B.2F- 1F C.1F+2F 图1-18 图1-19 1-3 F=100N,方向如图1-19 所示。若将 F 沿图示x,y 方向分解,则x 方向分力的大小 xF= C N,y 方向分力的大小yF= ___B __ N。 A. 86.6 B. 70.0 C. 136.6 D.25.9 1-4 力的可传性只适用于 A 。 A. 刚体 B. 变形体 1-5 加减平衡力系公理适用于 C 。 A. 刚体; B. 变形体; C. 刚体和变形体。 1-6 如图1-20 所示,已知一正方体,各边长 a,沿对角线BH 作用一个力F ,则该力在x1轴上的投影为 A 。 A. 0 B. F/2 C. F/6 D.-F/3 1-7 如图1-20 所示,已知 F=100N,则其在三个坐标轴上的投影分别为: Fx= -402 N ,Fy= 302 N ,Fz= 502 N 。 图 1 -2 0 图 1 -2 1 第二章 力系的简化 2-1.通过A(3,0,0),B(0,4,5)两点(长度单位为米),且由A 指向B 的力F,在z 轴上投影为 ,对z 轴的矩的大小为 。 答:F/2 ;62 F/5。 2-2.已知力F 的大小,角度φ 和θ ,以及长方体的边长a,b,c,则力F 在轴z 和y 上的投影:Fz= ;Fy= ;F 对轴x 的矩Mx( F )= 。 答:Fz=F·sinφ ;Fy=-F·cosφ ·cosφ ;Mx(F)=F(b·sinφ +c·cosφ ·cosθ ) 图2-40 图2-41 2-3.力F 通过A(3,4、0),B(0,4,4)两点(长度单位为米),若F=100N,则该力在x 轴上的投影为 ,对x 轴的矩为 。 答:-60N;320N.m 2-4.正三棱柱的底面为等腰三角形,已知OA=OB=a,在平面ABED 内有沿对角线AE的一个力F,图中α =30°,则此力对各坐标轴之矩为: Mx(F)= ;MY(F)= ;Mz(F)= 。 答:Mx(F)=0,My(F)=-Fa/2;Mz(F)=6 Fa/4 2-5.已知力F 的大小为60(N),则力F 对x 轴的矩为 ;对z 轴的矩为 。 答:Mx(F)=160 N·cm;Mz(F)=100 N·cm 图2-42 图2-43 2-6.试求图示中力F 对O 点的矩。 解:a: MO(F)=Flsinα b: MO(F)=Flsinα c: MO(F)=F(l1+l3)sinα+ Fl2cosα d: 2221llFFMosin 2-7.图示力F=1000N,求对于z轴的力矩Mz。 题2-7 图 题2-8 图 2-8.在图示平面力系中,已知:F1=10...