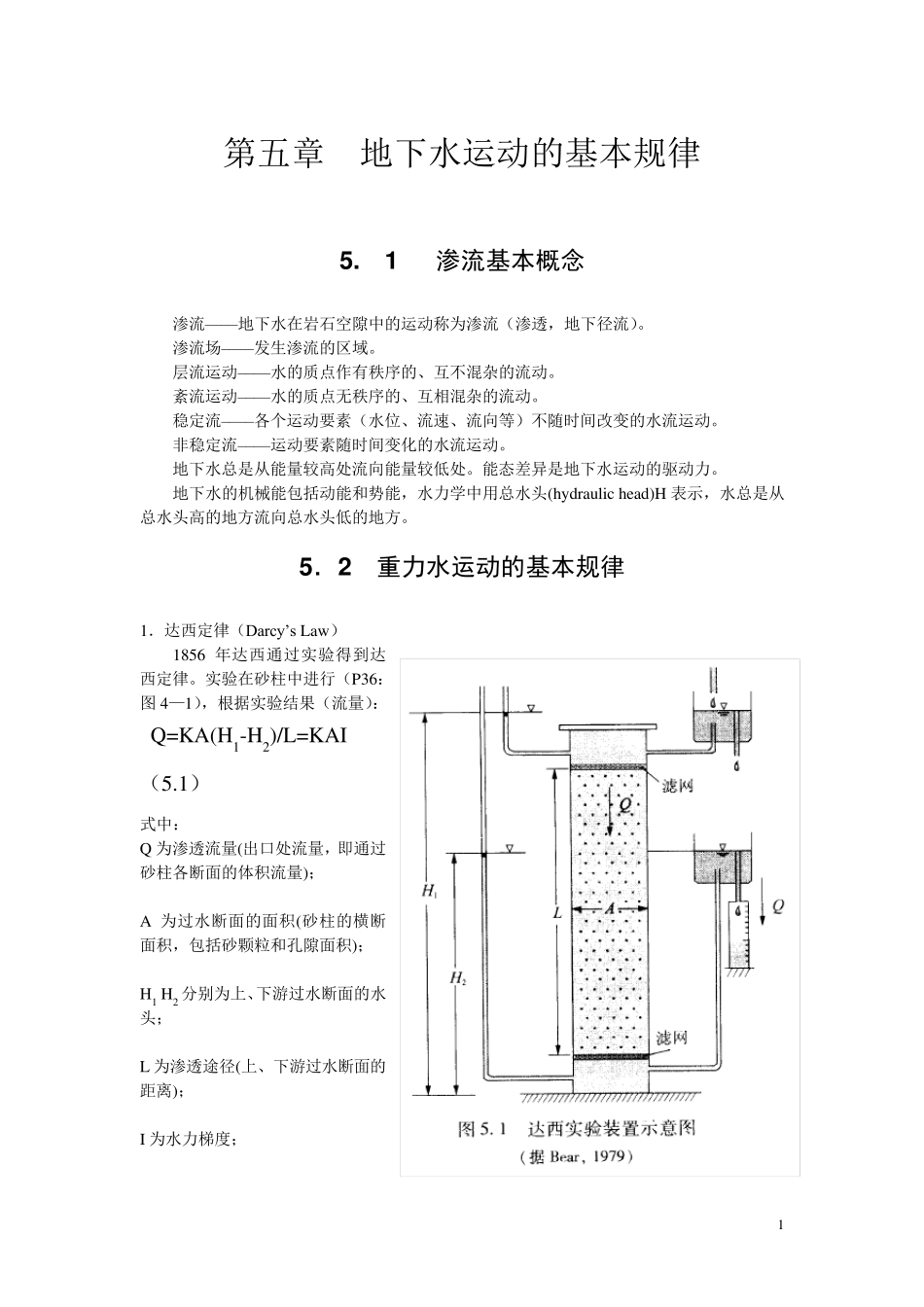
1 第五章 地下水运动的基本规律 5 . 1 渗流基本概念 渗流––––地下水在岩石空隙中的运动称为渗流(渗透,地下径流)。 渗流场––––发生渗流的区域。 层流运动––––水的质点作有秩序的、互不混杂的流动。 紊流运动––––水的质点无秩序的、互相混杂的流动。 稳定流––––各个运动要素(水位、流速、流向等)不随时间改变的水流运动。 非稳定流––––运动要素随时间变化的水流运动。 地下水总是从能量较高处流向能量较低处。能态差异是地下水运动的驱动力。 地下水的机械能包括动能和势能,水力学中用总水头(hydraulic head)H 表示,水总是从总水头高的地方流向总水头低的地方。 5 .2 重力水运动的基本规律 1.达西定律(Darcy’s Law) 1856 年达西通过实验得到达西定律。实验在砂柱中进行(P36:图4—1),根据实验结果(流量): Q=KA(H1-H2)/L=KAI (5.1) 式中: Q 为渗透流量(出口处流量,即通过砂柱各断面的体积流量); A 为过水断面的面积(砂柱的横断面积,包括砂颗粒和孔隙面积); H1 H2 分别为上、下游过水断面的水头; L 为渗透途径(上、下游过水断面的距离); I 为水力梯度; 2 K 为渗透系数。 由水力学:Q=vA 得到 v=Q/A (对地下水也适用) (5.2) 达西定律也可以另一种形式表达(流速): 由公式(5.1)及Q=VA 得: v=KI (5.3) 式中:V––––渗透流速,m/d,cm/s; K––––渗透系数,m/d,cm/s; I––––水力梯度,无量纲(比值)。 具体到实际问题: 计算流量: LHHKwQ21 (单位一般为:m3/d,L/s) 微分形式: dxdHKv 式中:负号表示水流方向与水力梯度方向相反,水流方向(坐标方向):由水位高→低;而水力梯度方向:由等水位线低→高。 在三维空间中(向量形式): KgradHkzHKjyHKixHKVzyx 或HKV, 式中:K––––为渗透系数张量; HkzHjyHixHgradH。 若用标量表示,V 的三个分量分别为: xHKvxx H1KLH2 3 yHKvyy zHKvzz 2.渗透流速(V)(seepage v elocity ,Darcy v elocity )与实际流速(u ) 渗透流速––––水流通过整个过水断面(包括砂砾和孔隙)的流速。 水流实际流过的面积(扣除结合水)––––水流实际过水断面是扣除结合水所占范围以外的空隙面积An 即: An =A ne (5.4) 式中:ne 为有效孔(空)隙度...