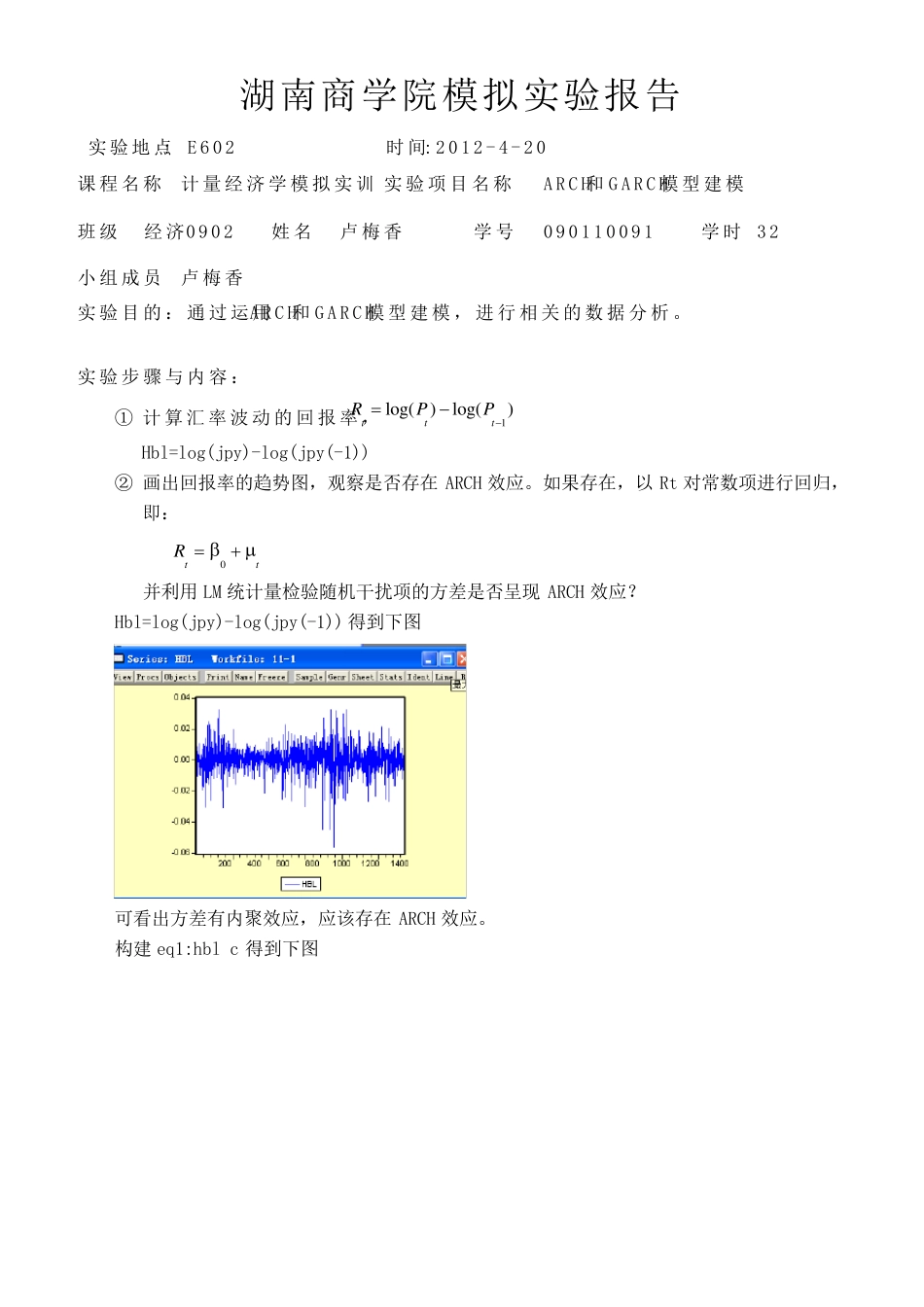
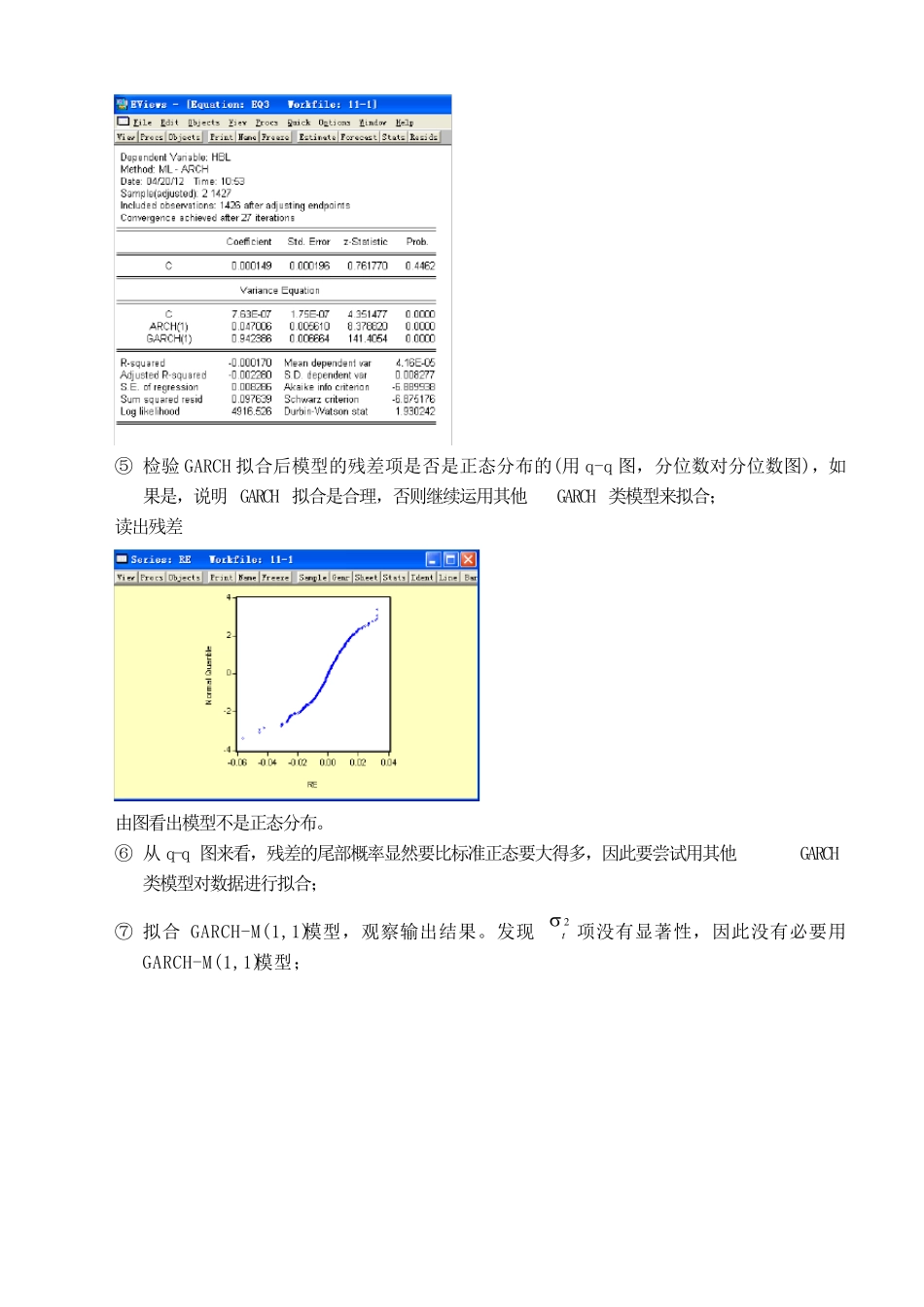
湖南商学院模拟实验报告 实验地点: E 6 0 2 时间: 2 0 1 2 - 4 - 2 0 课程名称 计量经济学模拟实训 实验项目名称 A R C H和G A R C H模型建模 班级 经济0 9 0 2 姓名 卢梅香 学号 0 9 0 1 1 0 0 9 1 学时 3 2 小组成员 卢梅香 实验目的:通过运用A R C H和G A R C H模型建模,进行相关的数据分析。 实验步骤与内容: ① 计算 汇 率 波 动 的回 报率 ,1lo g()lo g()tttRPP Hbl=log(jpy)-log(jpy(-1)) ② 画出回报率的趋势图,观察是否存在 ARCH 效应。如果存在,以 Rt 对常数项进行回归,即: 0ttR 并利用LM 统计量检验随机干扰项的方差是否呈现 ARCH 效应? Hbl=log(jpy)-log(jpy(-1)) 得到下图 可看出方差有内聚效应,应该存在 ARCH 效应。 构建eq1:hbl c 得到下图 由图看出存在ARCH 效应。 ③ 对回报率序列进行 ARCH 模型建模与估计,经反复计算,滞后阶选 2; 构建 eq2:hbl c 选 ARCH 模型建模与估计 Arch2 Garch0 得到下图 ④ 由于 ARCH 模型本身的局限性,我们对模型进行 GARCH(1,1)拟合; 构建 eq3:hbl c 对模型进行 GARCH(1,1)拟合,options 的收敛精度改为 1000 0.001 得到下图 ⑤ 检验 GARCH 拟合后模型的残差项是否是正态分布的(用 q-q 图,分位数对分位数图),如果是,说明 GARCH 拟合是合理,否则继续运用其他GARCH 类模型来拟合; 读出残差 由图看出模型不是正态分布。 ⑥ 从 q-q 图来看,残差的尾部概率显然要比标准正态要大得多,因此要尝试用其他GARCH类模型对数据进行拟合; ⑦ 拟合 GARCH-M(1,1)模型,观察输出结果。发现2t项没有显著性,因此没有必要用GARCH-M(1,1)模型; ⑧ 下面对序列进行 TARCH 拟合。在 Threshold 选项中设定滞后阶数为 1,结果发现 GARCH模型不存在新息冲击的非对称性,即不存在杠杆效应; ⑨ 拟合 EGARCH 模型。因为 TARCH 模型的设定是假设2t 对t 的影响是二次的,过于的简单且单一,应用 EGARCH 模型说明2t 对t 的影响是指数的,而不是二次的。C(3)是显著的,说明存在非对称的杠杆效应; ⑩ 进一步用成分 ARCH 模型拟合,再观察残差是否还存在 ARCH 效应。 实验结果与分析: 1、由图 1 可看出方差有内聚效应,应该存在 ARCH 效应 2、看残差的 ARCH 检验,可看出存在 ARCH 效应。 3、从 q-...