弧、弦、圆心角练习题及答案

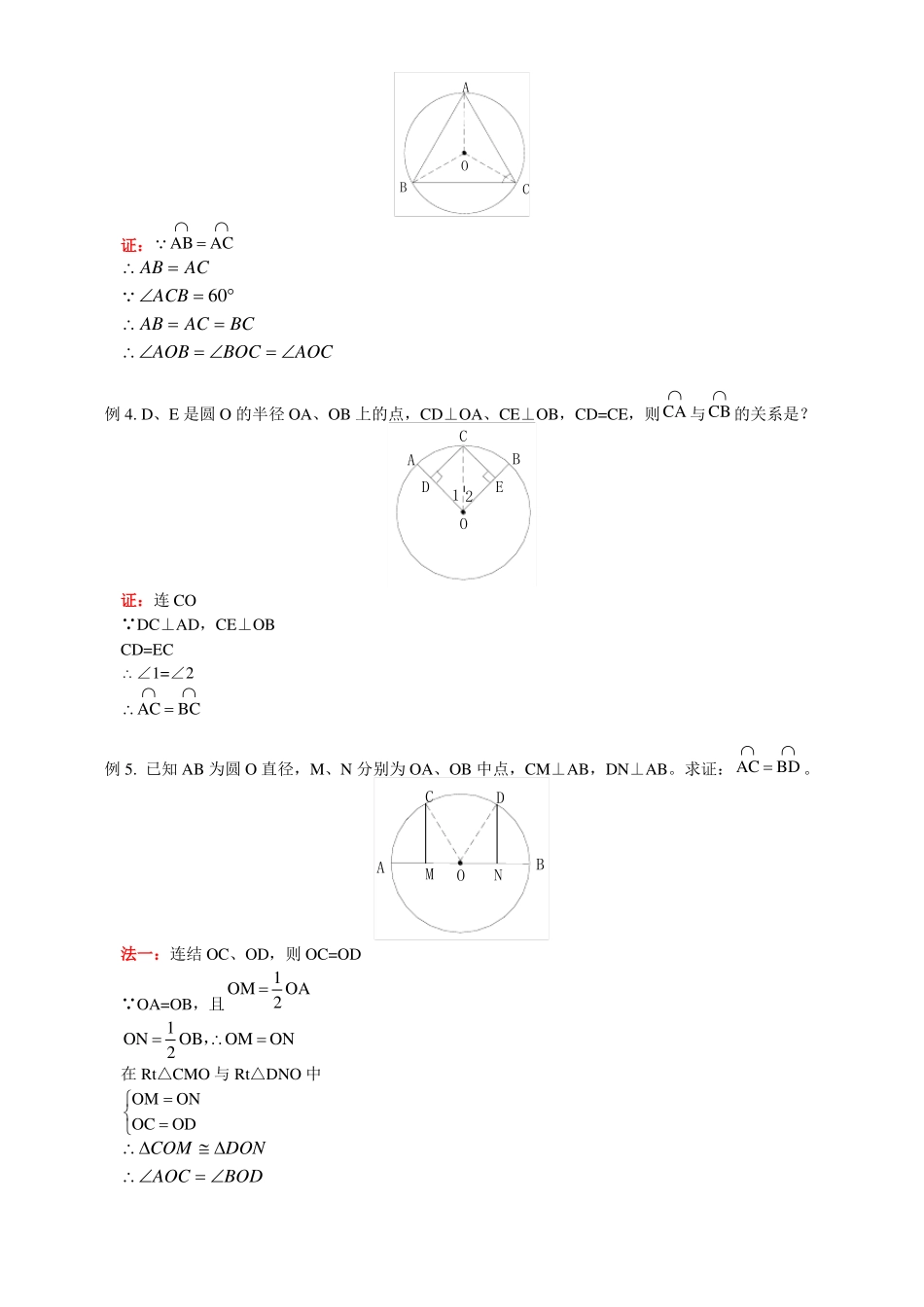
一.教学内容：弧、弦、圆心角二. 教学目标：1. 使学生理解圆的旋转不变性，理解圆心角、弦心距的概念；2. 使学生掌握圆心角、弧、弦、弦心距之间的相等关系定理及推论，并初步学会运用这些关系解决有关问题；3. 使学生理解并掌握 1°的弧的概念4. 培养学生观察、分析、归纳的能力，向学生渗透旋转变换的思想及由特殊到一般的认识规律.三. 教学重点、难点：圆心角、弧、弦、弦心距之间的相等关系是重点；从圆的旋转不变性出发，推出圆心角、弧、弦、弦心距之间的相等关系是难点。四. 教学过程设计：1. 圆的旋转不变性圆是轴对称图形。也是中心对称图形。不论绕圆心旋转多少度，都能够和原来的图形重合。圆所特有的性质——圆的旋转不变性圆绕圆心旋转任意一个角度α，都能够与原来的图形重合。2. 圆心角，弦心距的概念.顶点在圆心的角叫做圆心角。弧 AB 是∠AOB 所对的弧，弦 AB 既是圆心角∠AOB 也是弧 AB 所对的弦.圆心到弦的距离叫做弦心距。3. 圆心角、弧、弦、弦心距之间的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。同样还有：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都也相等。4. 1°的弧的概念. (投影出示图 7－59)圆心角的度数和它所对的弧的度数相等。这里指的是角与弧的度数相等，而不是角与弧相等。即不能写成圆∠AOB=，这是错误的。【典型例题】例 1. 判断题，下列说法正确吗？为什么？（1）如图所示：因为∠AOB=∠A′OB′，所以=.（2）在⊙O 和⊙O′中，如果弦 AB=A′B′，那么=。分析：（1）、（2）都是不对的。在图中，因为不在同圆或等圆中，不能用定理。对于（2）也缺少了等圆的条件. 可让学生举反例说明。例 2. 已知：如图所示，AD=BC。求证：AB=CD。证： AD=BCAD  BCAC  ACAC AD  AC BCDC  ABAB  DC变式练习。已知：如图所示，=，求证：AB=CD。证： AD  BC DA AC  BC ACAC  ACDC  ABAB  CDACB  60例 3. 在圆 O 中，AB  AC求证：∠AOB=∠BOC=∠AOCAOBC证：AB  AC AB  ACACB  60 AB...