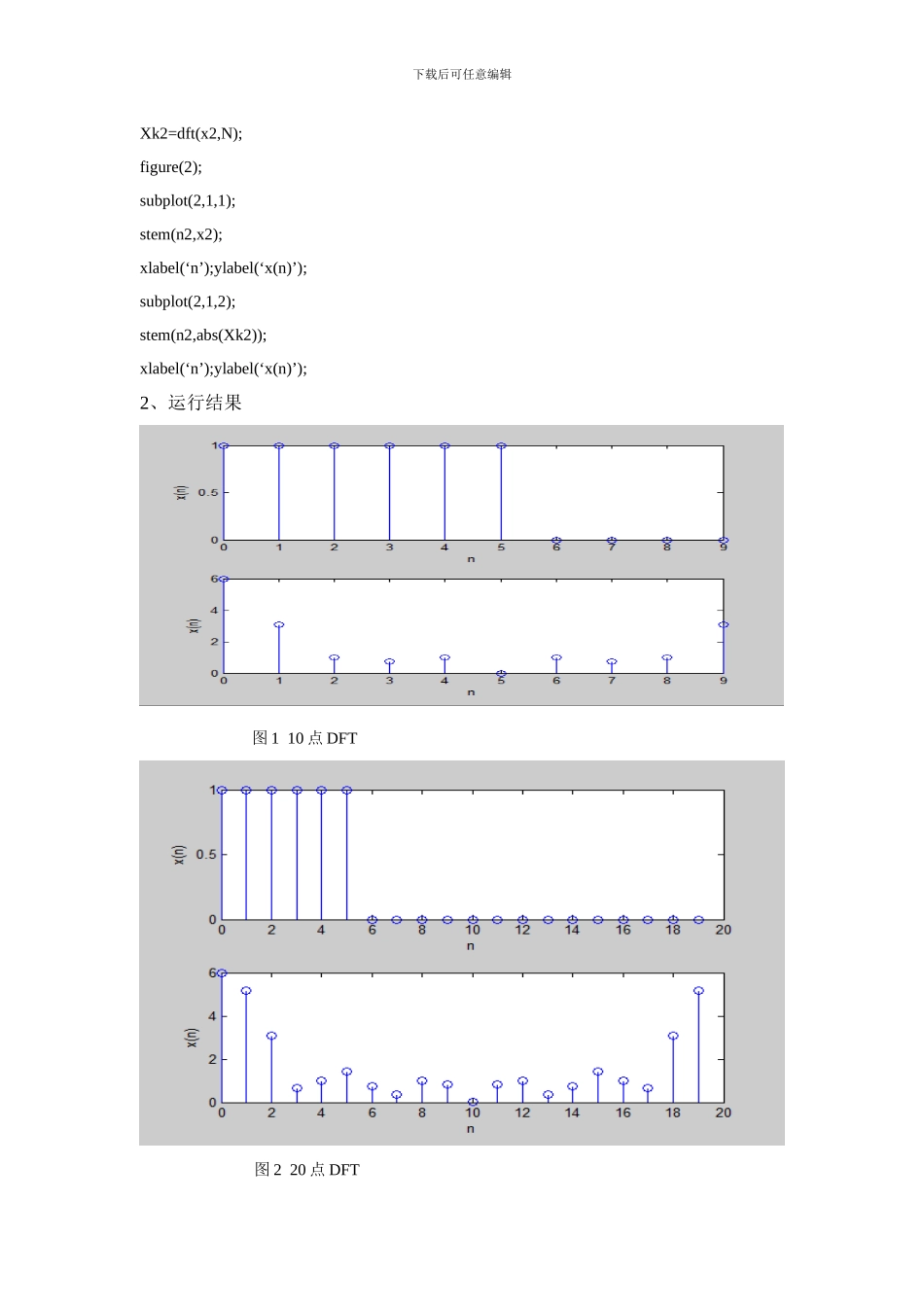
下载后可任意编辑XXXX 大学实验报告XXXX 年 XX 月 XX 日课程名称: 数字信号处理 实验名称:用 FFT 作谱分析 班级: XXXXXXXX 班 学号: XXXXXXXX 姓名: XXXX 实验三 用 FFT 作谱分析一、实验目的(1) 进一步加深 DFT 算法原理和基本性质的理解(因为 FFT 只是 DFT 的一种快速算法,所以 FFT 的运算结果必定满足 DFT 的基本性质);(2) 熟悉 FFT 算法的原理;(3) 学习用 FFT 对连续信号和时域离散信号进行谱分析的方法分析误差及其原因,以便在实际中正确应用 FFT。二、实验内容 (1)x(n)={10≤n≤50其他 构造 DFT 函数计算 x(n)的 10 点 DFT,20 点 DFT 并画出图形; (2)利用 FFT 对下列信号逐个进行谱分析并画出图形 a、x1(n)=R4(n); b、x2(n)=cosπ4 n; c、x3(n)=sinπ8 n 以上 3 个序列的 FFT 变换区间 N=8,16(2)设一序列中含有两种频率成份,f1=2HZ,f2=2.05HZ,采样频率取为 fs=10HZ,即x(n)=sin(2 πf 1n/f s)+sin(2πf 2n/f s) 要区分出这两种频率成份,必须满足 N>400,为什么?a.取 x(n)(0≤n<128)时,计算 x(n)的 DFT X(k)b.将 a 中的 x(n)以补零方式使其加长到 0≤n<512,计算 X(k)下载后可任意编辑c.取 x(n)( 0≤n<512),计算 X(k)(3)令x(n)=x2(n)+x3(n)用 FFT 计算 16 点离散傅立叶变换并画出图形,分析 DFT 的对称性(4)x(n)=x2(n)+ jx3(n)用 FFT 计算 16 点离散傅立叶变换并画出图形,分析 DFT 的对称性三、实验代码(1)1、 代码 function[Xk]=dft(xn,N) n=[0:1:N-1];k=[0:1:N-1];WN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^nk;Xk=xn*WNnk; %离散傅立叶变换方法定义N=10; %10 点 DFTn1=[0:N-1];x1=[ones(1,6),zeros(1,N-6)]; %生成 1 行 6 列的单位矩阵和 1 行 N-6 列的 0 矩阵Xk1=dft(x1,N); %10 点 DFTfigure(1);subplot(2,1,1);stem(n1,x1); %画火柴图xlabel(‘n’);ylabel(‘x(n)’);subplot(2,1,2);stem(n1,abs(Xk1));xlabel(‘n’);ylabel(‘x(n)’);N=20;n2=[0:N-1];x2=[ones(1,6),zeros(1,14)];下载后可任意编辑Xk2=dft(x2,N);figure(2);subplot(2,1,1);stem(n2,x2);xlabel(‘n’);ylabel(‘x(n)’);subplot(2,1,2);stem(n2,abs(Xk2));xlabel(‘n’);ylabel(‘x(n)’);2、运行结果 图 1 10 点 DFT 图 2 20 点 DFT下载后可任意编辑3、结果分析定义 x(n)的 N 点 DFT ...