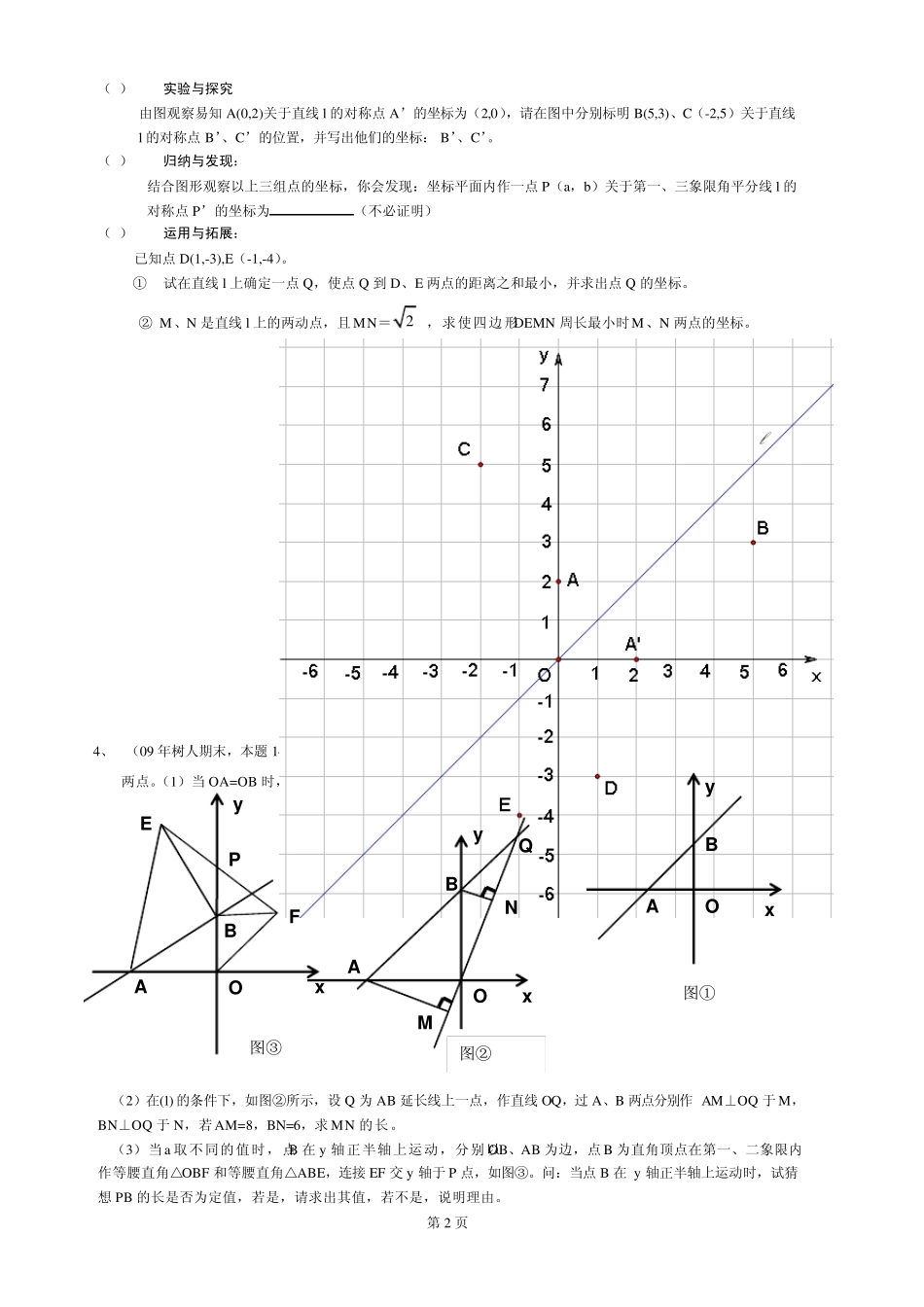
第1 页 1、 (06 年树人期末,14 分) 如图,在直角坐标系中,四边形OABC 为直角梯形,OA∥BC,BC=14,A(16,0),C(0,2)。(单位:厘米)若点P、Q 分别从C、A 同时出发,点P 以2cm/s 速度由C 向B 运动,点Q 以4cm/s 速度由A 向O 运动,当点Q 停止运动时,点P 也停止运动。设运动时间为t s(0 t< =4)。(1)求当t 为多少时,四边形PQAB 为平行四边形; (2)求当t 为多少时,直线PQ 将梯形OABC 分成左右两部分的面积比为1:2,求出此时直线PQ 的解析式; xyQPCBAO (3)点P、Q 为线段BC、AO 上任意两点(不与线段BC、AO 的端点重合),且四边形OQPC 的面积为102cm,试说明直线PO 一定经过一定点,并求出定点坐标 xyQPCBAO 2、 (07 年树人期末,14 分) 如图①,在矩形 ABCD 中,AB=10cm,BC=8cm.点P 从A 出发,沿A、B、C、D 路线运动,到D 停止;点Q 从D 出发,沿 D→C→B→A路线运动,到A 停止.若点P、点Q 同时出发,点P 的速度为每秒 1cm,点Q 的速度为每秒 2cm,a 秒时点P、点Q 同时改变速度,点P 的速度变为每秒 bcm,点Q 的速度变为每秒 dcm.图②是点P 出发x 秒后上△APD 的面积S1(2cm)与x(秒)的函数关系图象;图③是点Q 出发x 秒后△AQD 的面积S2(2cm)与x(秒)的函数关系图象.⑴ 参照图②,求a、b 及图②中c 的值; ⑵ 求d 的值;⑶ 设点P 离开点A 的路程为y 1(cm),点Q 到点A 还需走的路程为y 2(cm),请分别写出动点P、Q 改变速度后 y 1、y 2 与出发后的运动时间x(秒)的函数关系式,并求出P、Q 相遇时x 的值. ⑷ 当点Q 出发 秒时,点P、点Q 在运动路线上相距的路程为25cm. 3、 (08 年树人期末,14 分) 1、 如图,在平面直角坐标系中,直线l 是第一、三象限的角平分线。 第2 页 (1) 实验与探究 由图观察易知A(0,2)关于直线l 的对称点A’的坐标为(2,0),请在图中分别标明 B(5,3)、C(-2,5)关于直线l 的对称点B’、C’的位置,并写出他们的坐标: B’、C’。 (2) 归纳与发现: 结合图形观察以上三组点的坐标,你会发现:坐标平面内作一点P(a,b)关于第一、三象限角平分线l 的对称点P’的坐标为 (不必证明) (3) 运用与拓展: 已知点D(1,-3),E(-1,-4)。 ① 试在直线l 上确定一点Q,使点Q 到 D、E 两点的距离之和最小,并求出点Q 的坐标。 ② M、N 是直线l 上的两动点,...