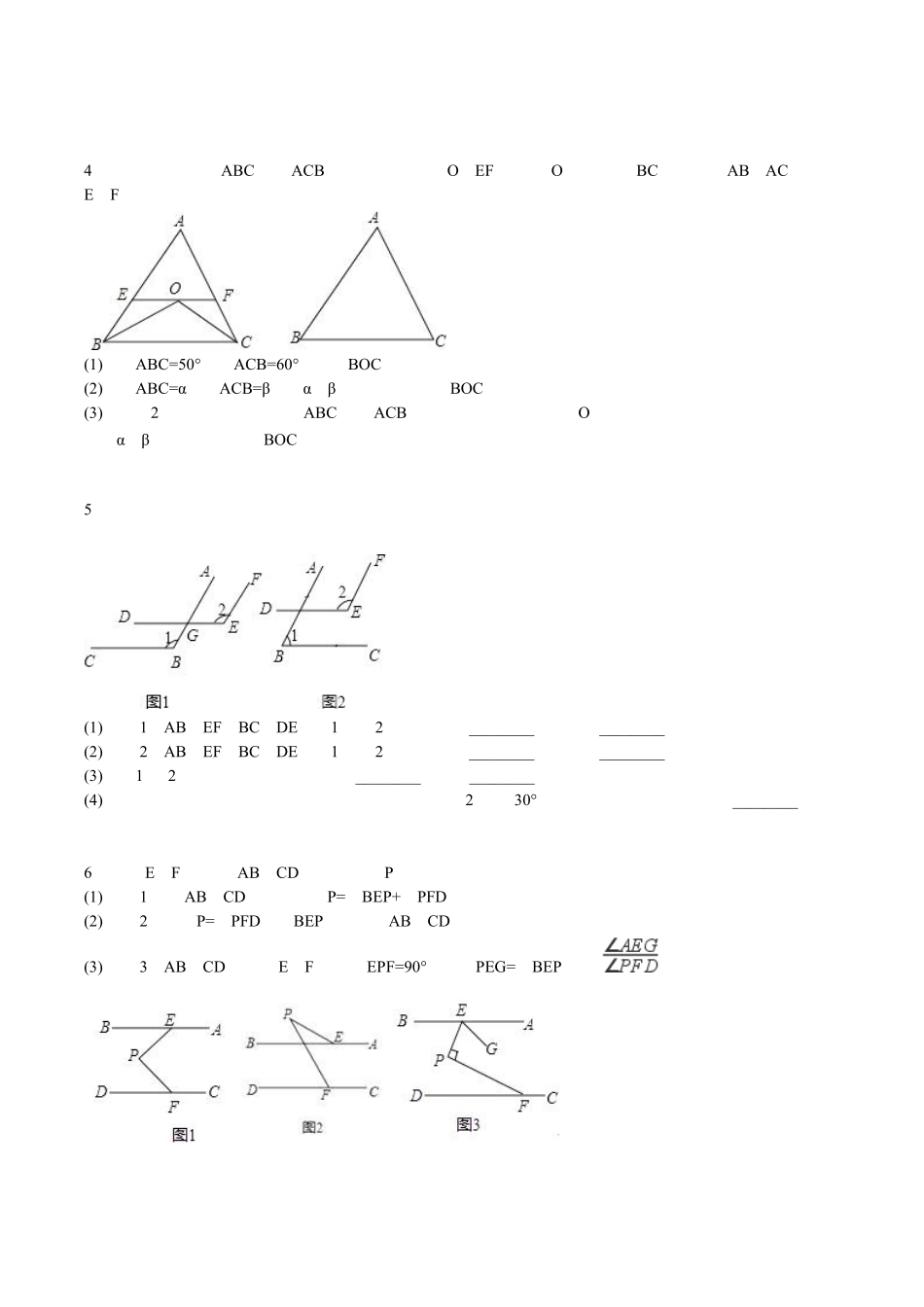
1、如图,已知 l1∥l2,MN 分别和直线 l1、l2 交于点 A、B,ME 分别和直线 l1、l2 交于点 C、D,点 P 在 MN上(P 点与 A、B、M 三点不重合).(1)如果点 P 在 A、B 两点之间运动时,∠α、∠β、∠γ之间有何数量关系请说明理由;(2)如果点 P 在 A、B 两点外侧运动时,∠α、∠β、∠γ有何数量关系(只须写出结论).2、如图,已知 AM∥BN,∠A=60°.点 P 是射线 AM 上一动点(与点 A 不重合),BC、BD 分别平分∠ABP和∠PBN,分别交射线 AM 于点 C,D.(1)求∠CBD 的度数;(2)当点 P 运动时,∠APB 与∠ADB 之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(3)当点 P 运动到使∠ACB=∠ABD 时,∠ABC 的度数是.3、已知直线 AB∥CD.(1)如图 1,直接写出∠ABE,∠CDE 和∠BED 之间的数量关系是.(2)如图 2,BF,DF 分别平分∠ABE,∠CDE,那么∠BFD 和∠BED 有怎样的数量关系?请说明理由.(3)如图 3,点 E 在直线 BD 的右侧,BF,DF 仍平分∠ABE,∠CDE,请直接写出∠BFD 和∠BED 的数量关系.3、如图,AB∥CD,E 为 AB 上一点,∠BED=2∠BAD.(1)求证:AD 平分∠CDE;(2)若 AC⊥AD,∠ACD+∠AED=165°,求∠ACD 的度数.4、已知:如图,∠ABC 和∠ACB 的平分线交于点 O,EF 经过点 O 且平行于 BC,分别与 AB,AC 交于点E,F.(1)若∠ABC=50°,∠ACB=60°,求∠BOC 的度数;(2)若∠ABC=α,∠ACB=β,用α,β的代数式表示∠BOC 的度数.(3)在第(2)问的条件下,若∠ABC 和∠ACB 邻补角的平分线交于点 O,其他条件不变,请画出相应图形,并用α,β的代数式表示∠BOC 的度数.5、已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的关系,并说明你的结论.(1)如图 1,AB∥EF,BC∥DE.∠1 与∠2 的关系是:________,理由:________;(2)如图 2,AB∥EF,BC∥DE.∠1 与∠2 的关系是:________,理由:________.(3)由(1)(2)你得出的结论是:如果________,那么________.(4)若两个角的两边互相平行,且一个角比另一个角的 2 倍少 30°,则这两个角度数的分别是________6、已知 E,F 分别是 AB、CD 上的动点,P 也为一动点.(1)如图 1,若 AB∥CD,求证:∠P=∠BEP+∠PFD;(2)如图 2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD;(3)如图 3,...