三角函数图像与性质讲义

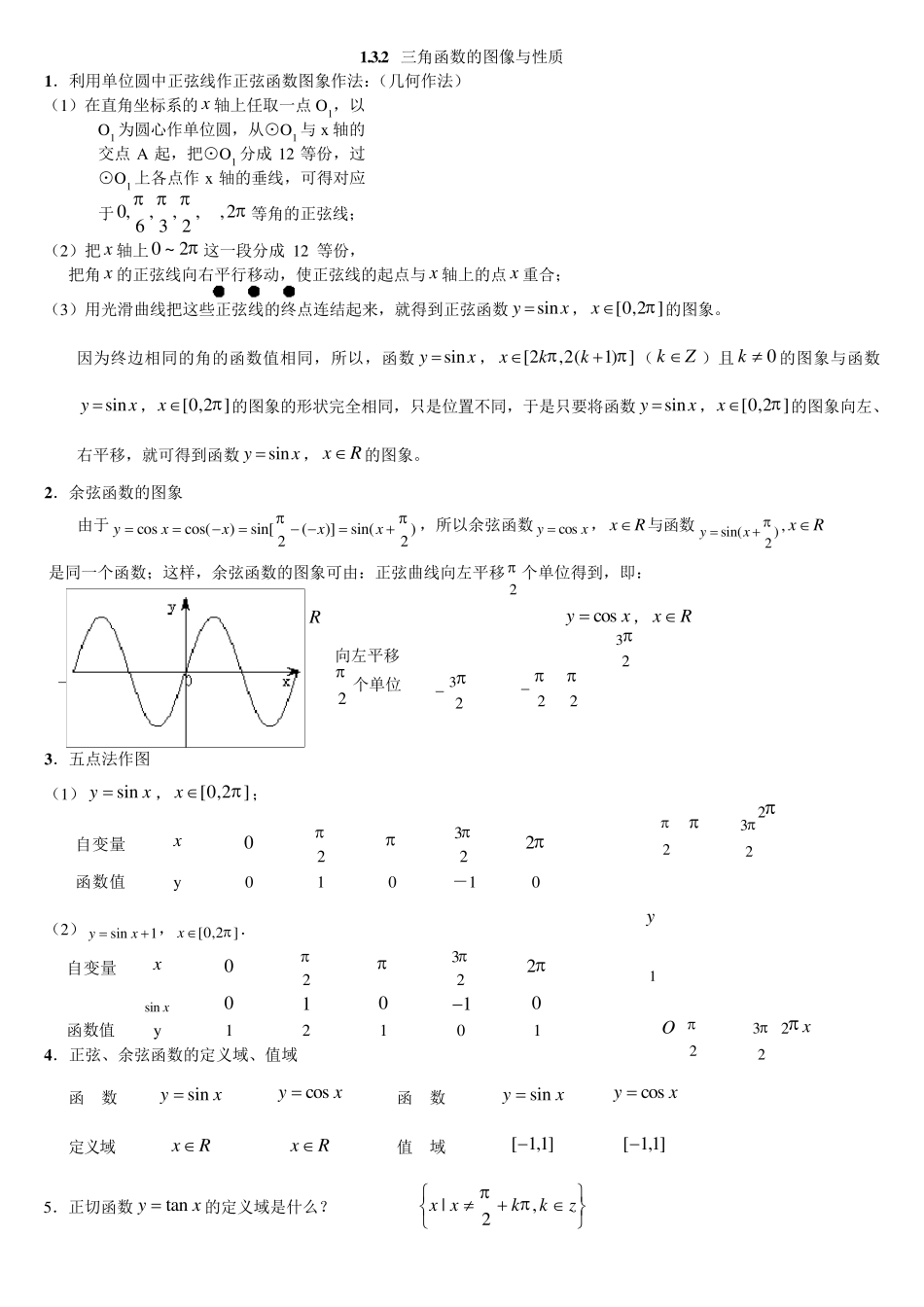
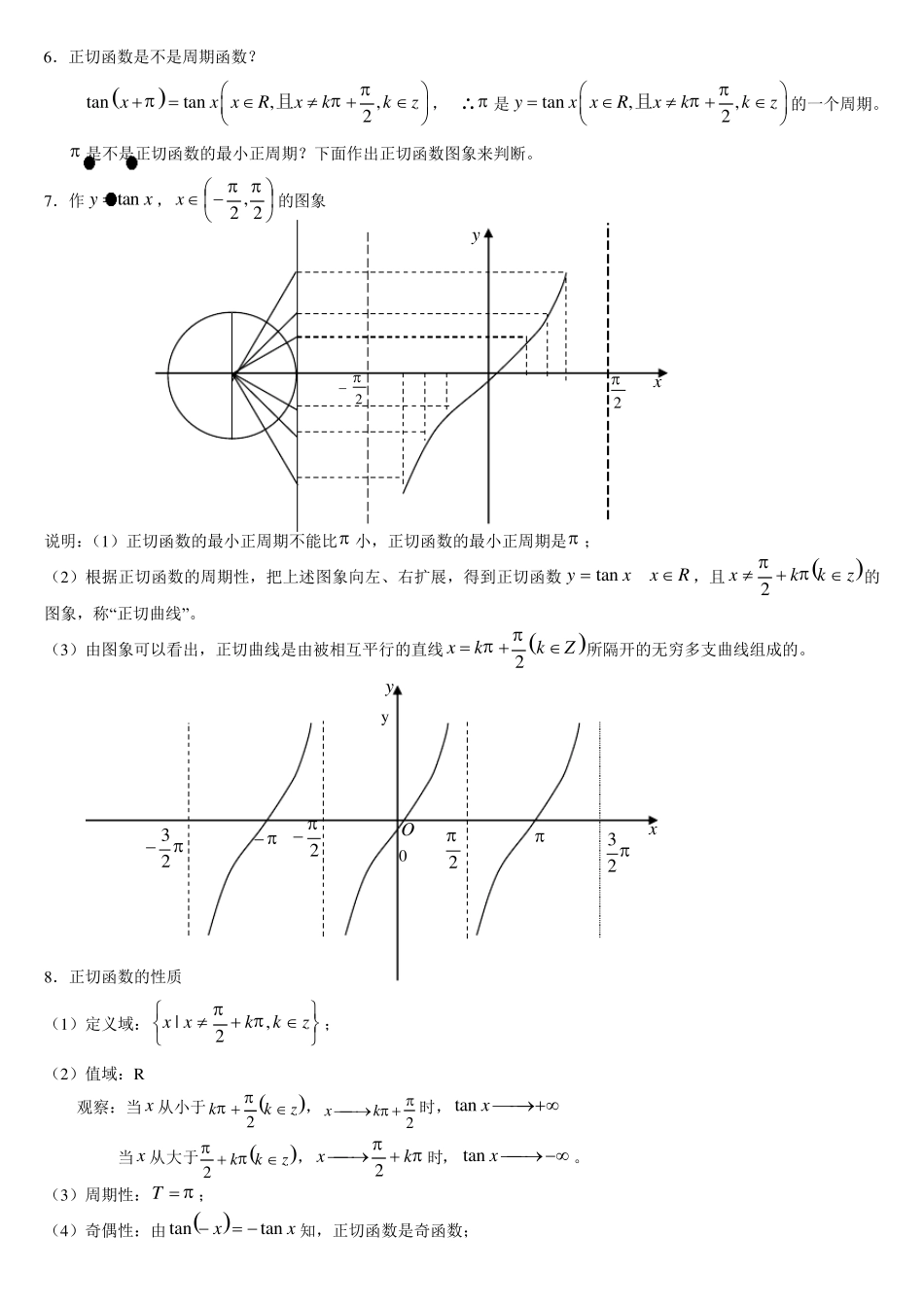
sinyx，xR   2 cosyx，xR 2 32 2 32 1 .3 .2 三角函数的图像与性质 1 ．利用单位圆中正弦线作正弦函数图象作法：（几何作法） （1）在直角坐标系的x 轴上任取一点O1，以O1 为圆心作单位圆，从⊙O1 与x 轴的交点A 起，把⊙O1 分成 12 等份，过⊙O1 上各点作x 轴的垂线，可得对应于0,,,,,26 3 2   等角的正弦线； （2）把 x 轴上0 ~ 2 这一段分成 12 等份，把角x 的正弦线向右平行移动，使正弦线的起点与x 轴上的点x 重合； （3）用光滑曲线把这些正弦线的终点连结起来，就得到正弦函数sinyx，[0,2 ]x的图象。 因为终边相同的角的函数值相同，所以，函数sinyx，[2,2(1) ]xkk（kZ）且0k 的图象与函数sinyx，[0,2 ]x的图象的形状完全相同，只是位置不同，于是只要将函数sinyx，[0,2 ]x的图象向左、右平移，就可得到函数sinyx，xR的图象。 2 ．余弦函数的图象 由于coscos()sin[()]sin()22yxxxx ，所以余弦函数cosyx，xR与函数sin()2yx, xR 是同一个函数；这样，余弦函数的图象可由：正弦曲线向左平移2 个单位得到，即： 3 ．五点法作图 （1）sinyx，[0,2 ]x； 自变量 x 0 2  32 2 函数值 y 0 1 0 －1 0 （2）sin1yx ，[0,2 ]x． 自变量 x 0 2  32 2 sin x 0 1 0 1 0 函数值 y 1 2 1 0 1 4 ．正弦、余弦函数的定义域、值域 函 数 sinyx cosyx 函 数 sinyx cosyx 定义域 xR xR 值 域 [ 1,1] [ 1,1] 5．正切函数tanyx的定义域是什么？ zkkxx,2| y x O 32 1 2 2 向左平移 2 个单位 32 2  2 6．正切函数是不是周期函数？ tantan,,2xx xRxkkz且， ∴ 是tan,,2yx xRxkkz且的一个周期。  是不是正切函数的最小正周期？下面作出正切函数图象来判断。 7．作tanyx，x2,2的图象 说明：（1）正切函数的最小正周期不能比 小，正切函数的最小正周期是 ； （2）根据正切函数的周期性，把上述图象向左、右扩展，得到正切函数Rxxy tan，且zkkx2的图象，称“正切曲线”。 （3）由图象可...