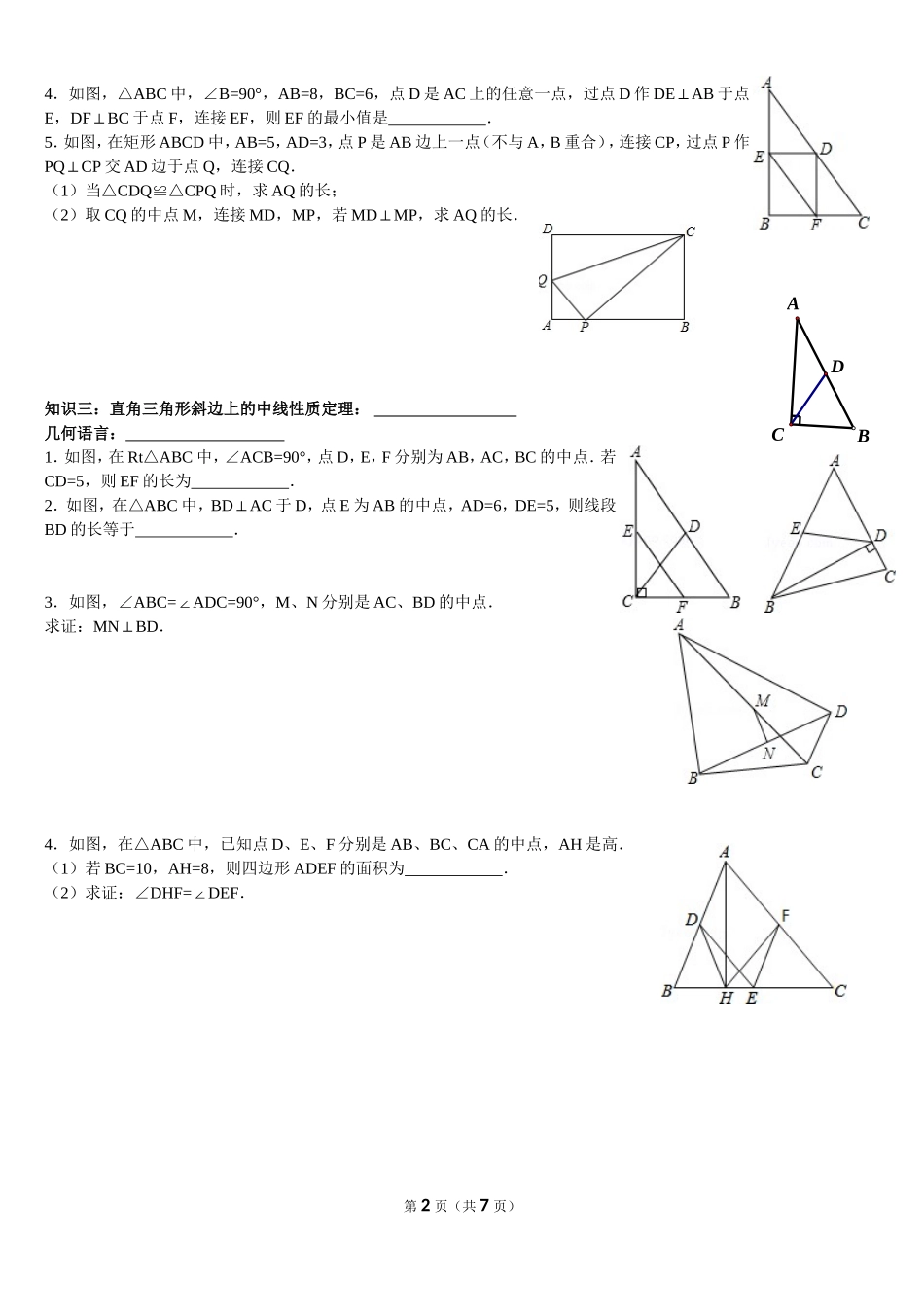
中位线 矩形的性质与判定 一:知识点 1,中位线的性质定理: 几何语言: 针对训练:1.如图,△ABC 的中线 BD、CE 交于点 O,连接 OA,点 G、F 分别为 OC、OB 的中点 ,BC=8,AO=6,则四边形 DEFG 的周长为( )A.12 B.14C.16D.182.如图,在△ABC 中,D,E 分别是 AB,AC 的中点,AC=12,F 是 DE 上一点,连接 AF,CF,DF=1.若∠AFC=90°,则 BC的长度为( )A.12 B.13C.14D.153.如图,四边形 ABCD 中,∠A=90°,AB=3,AD=3,点 M,N 分别为线段 BC,AB 上的动点(含端点,但点 M 不与点 B重合),点 E,F 分别为 DM,MN 的中点,则 EF 长度的最大值为 .4.如图,在△ABC 中,AB=5,AC=3,AD、AE 分别为△ABC 的中线和角平分线,过点 C 作 CHAE⊥于点 H,并延长交 AB于点 F,连结 DH,则线段 DH 的长为 .5.如图,等边△ABC 的边长是 2,D、E 分别为 AB、AC 的中点,延长 BC 至点 F,使 CF= BC,连接 CD 和 EF.(1)求证:DE=CF;(2)求 EF 的长.知识点二7.3.1.矩形的概念: 的平行四边形是矩形.7.3.2.矩形的性质(1)具有 四边形的一切性质;(2)矩形的四个角都是 .(3)矩形的对角线 ;(4)矩形是 图形.7.2.3.矩形的判定(1)定义: 的平行四边形是矩形.(2)定理 1: 的四边形是矩形.(3)定理 2: 的平行四边形是矩形.针对训练:1.如图,在矩形 ABCD 中,M、N 分别是边 AD、BC 的中点,E、F 分别是线段 BM、CM 的中点.若AB=8,AD=12,则四边形 ENFM 的周长为 .2.如图,在平面直角坐标系中,O 为坐标原点,矩形 OABC 中,A(10,0),C(0,4),D 为 OA 的中点,P 为 BC 边上一点.若△POD 为等腰三角形,则所有满足条件的点 P 的坐标为 .3.如图,矩形 ABCD 中,AB=2,BC=4,点 A、B 分别在 y 轴、x 轴的正半轴上,点 C 在第一象限,如果∠OAB=30°,那么点C 的坐标是 .第 1 页(共 7 页)ODBCAABCDE4.如图,△ABC 中,∠B=90°,AB=8,BC=6,点 D 是 AC 上的任意一点,过点 D 作 DEAB⊥于点E,DFBC⊥于点 F,连接 EF,则 EF 的最小值是 .5.如图,在矩形 ABCD 中,AB=5,AD=3,点 P 是 AB 边上一点(不与 A,B 重合),连接 CP,过点 P 作PQCP⊥交 AD 边于点 Q,连接 CQ.(1)当△CDQCPQ≌△时,求 AQ 的长;(2)取 CQ 的中点 M,连接 MD,MP,若 MDM...