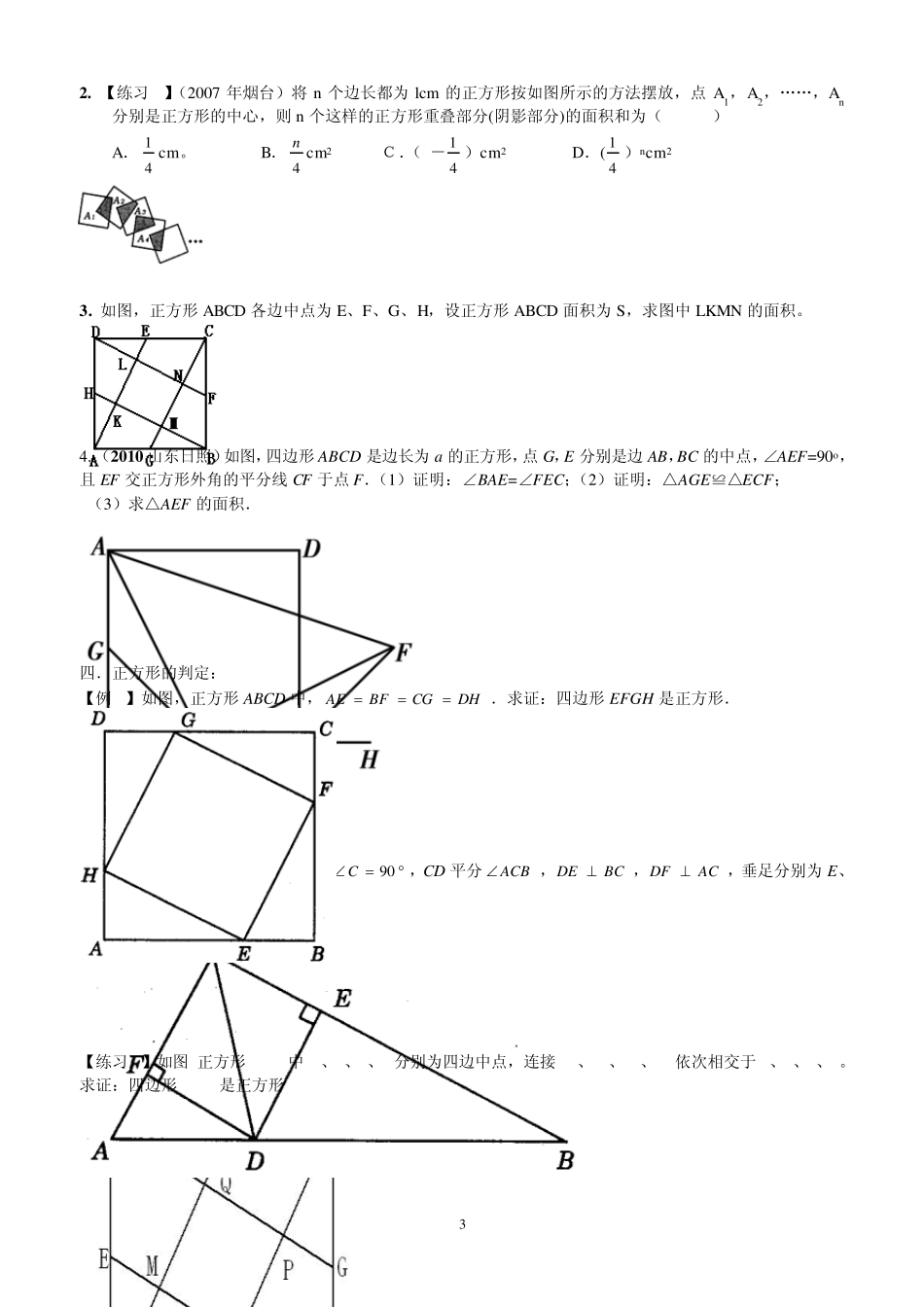
1 专题训练----正方形(2012.5.) 一.正方形的性质: 【例 1】(2008 湖北襄樊)如图 12,B、C、E 是同一直线上的三个点,四边形 ABCD 与四边形 CEFG 是都是正方形.连接 BG、DE.(1)观察猜想 BG 与 DE 之间的大小关系,并证明你的结论.(2)在图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由. 【例 2】如图,E 是正方形 ABCD 边 BC 延长线上一点,CE=AC,AE 交 CD 于 F,求∠AFC 的度数。 【例 3】如图 4-60,正方形 ABCD的对角线相交于 O,EF∥AB,并且分别与 OA,OB相交于 E,F.若 BE=3厘米,求 CF的长. 【练习 1】(2008年沈阳市)如图所示,正方形中,点是边上一点,连接,交对角线于点,连接,则图中全等三角形共有( ) A.1 对 B.2 对 C.3 对 D.4 对 【练习 2】(2 0 1 0 天津)如图,已知正方形 ABC D 的边长为 3,E 为 C D 边上一点, 1D E .以点 A 为中心,把△ AD E 顺时针旋转 90 ,得△ ABE ,连接 EE ,则 EE 的长等于 . 【练习 3】(2008 佛山 12)如图,已知 P 是正方形 ABCD 对角线 BD 上一点,且 BP = BC,则∠ACP 度数是 . 【练习 4】(2005 山西) 如图 1,正方形 ABCD 的边 CD 在正方形 ECGF 的边 CE 上,连结 BE、DG.(1) 观察猜想 BE 与 DC 之间的大小关系,并说明你的结论; (2) 图中是否存在通过旋转能够互相重合的两个三角形? 若存在,请说出旋转过程; 若不存在,请说明理由. 【练习 5】(2008 广东肇庆市)如图 5,在等腰Rt△ABC 中,∠C=90°, 正方形 DEFG 的顶点 D 在边 AC 上,点 E、F 在边 AB 上,点 G 在边 BC 上. (1)求证 AE=BF; (2)若 BC=cm,求正方形 DEFG 的边长. 2 M D Q C N B A 【练习6】(2010湖南长沙)在正方形 ABCD中,AC为对角线,E为 AC上一点,连接 EB、ED (1)求证:△BEC≌△DEC;(2)延长 BE交 AD于 F,当∠BED=120°时,求E F D的度数. 【练习7】(2010 四川宜宾)如图,点P 是正方形ABCD 的对角线BD 上一点,PE⊥BC 于点E,PF⊥CD 于点F,连接EF 给出下列五个结论:①AP =EF;②AP⊥EF;③△APD 一定是等腰三角形; ④∠PFE=∠BAP;⑤PD= 2EC.其中正确结论的序号是 . 二.正方形的折纸: 【例1】(08 哈尔...