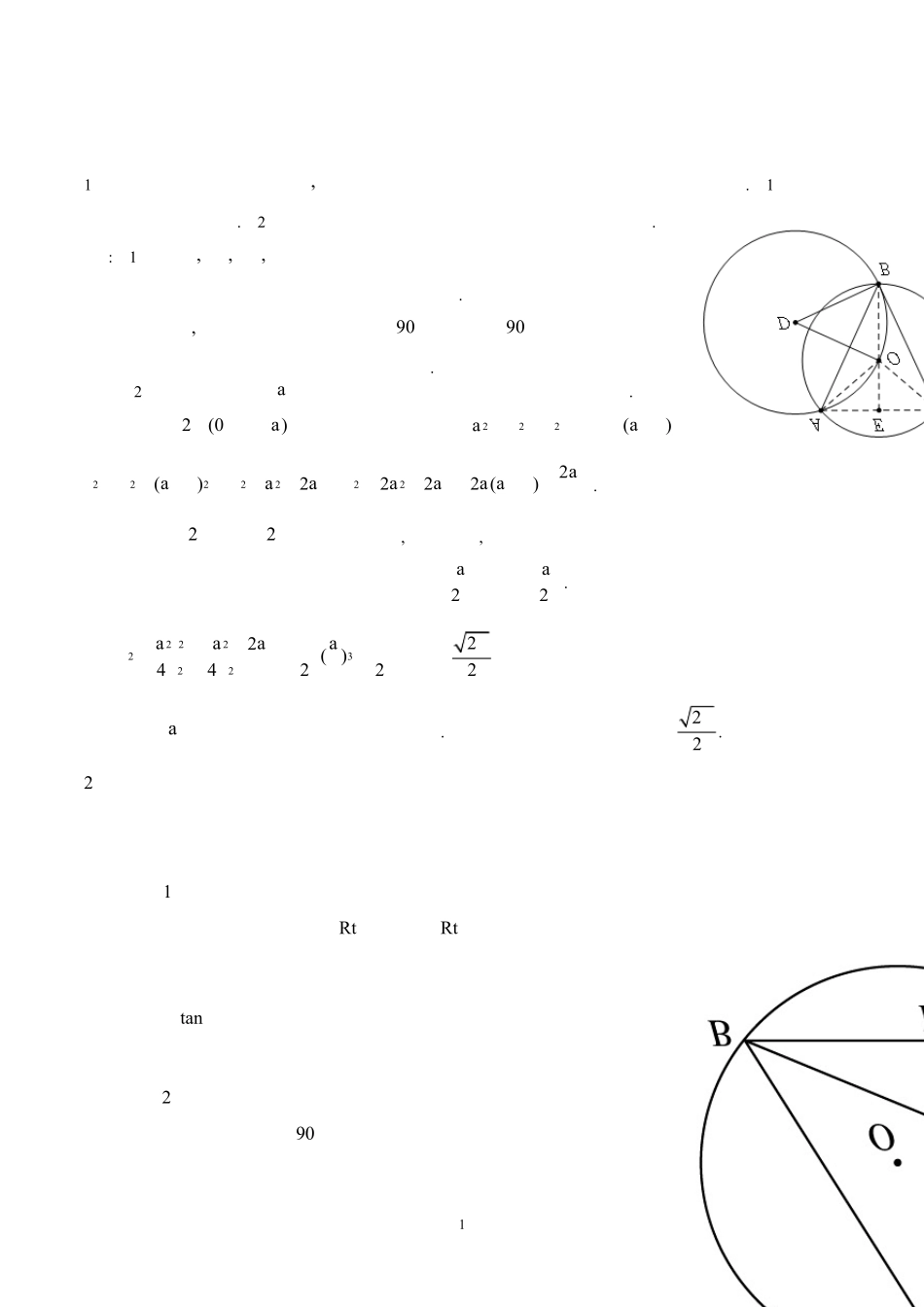
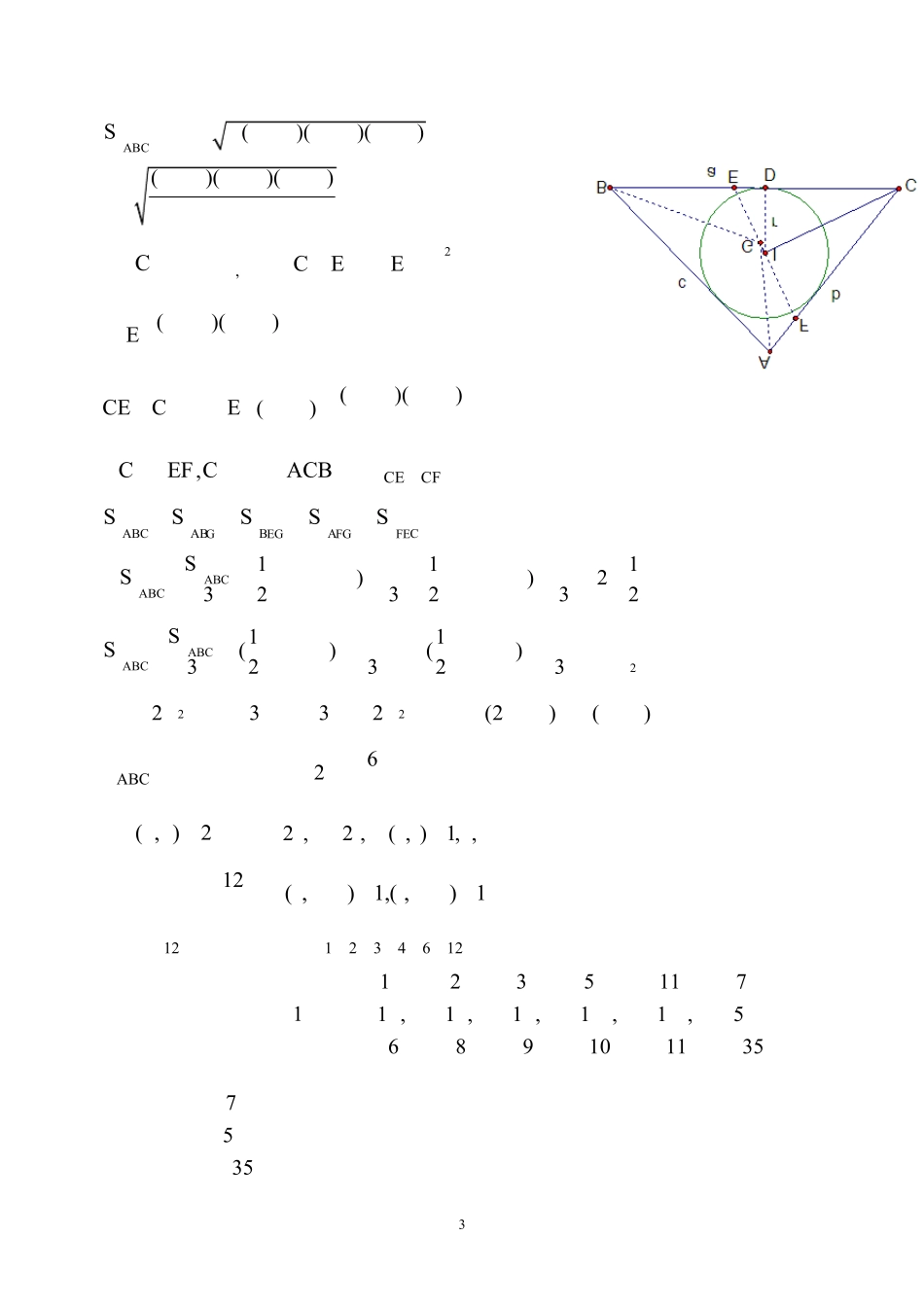
1全国初中数学竞赛试题汇编---几何解答题1、如图,圆O与圆 D相交于 ,AB两点, BC为圆 D的切线,点C在圆O上,且 AB BC=.(1)证明:点O在圆 D的圆周上.(2)设△ ABC的面积为 S,求圆 D的的半径r的最小值.解 :(1)连,,,OAOBOCAC,因为O为圆心, AB BC=,所以△OBA∽△OBC,从而OBA OBC∠=∠.因为,OD ABDB BC⊥⊥,所以9090DOBOBAOBC DBO∠= °−∠= °−∠=∠,所以 DB DO=,因此点O在圆 D的圆周上.(2)设圆O的半径为a , BO的延长线交 AC于点 E,易知 BE AC⊥.设2ACy=(0)y a< ≤,OE x= , AB l= ,则222axy=+,()S yax=+,22222222()2222 ()aSlyaxy aax xaaxa axy=+ +=+++=+=+=.因为22ABCOBAOAB BDO∠= ∠= ∠=∠, AB BC=, DB DO=,所以△ BDO∽△ ABC,所以 BD BOAB AC=,即2raly=,故2alry=.所以2 2223222( )4422a laaS S aSryyyy==⋅= ⋅≥,即22Sr≥,其中等号当 ay= 时成立,这时 AC是圆O的直径.所以圆 D的的半径 r的最小值为22S.2、如图,给定锐角三角形 ABC, BC CA<,AD,BE是它的两条高,过点 C作△ABC的外接圆的切线l,过点 D,E分别作l的垂线,垂足分别为 F,G.试比较线段 DF和 EG的大小,并证明你的结论.解法 1:结论是 DF EG=.下面给出证明.因为FCD EAB∠=∠,所以 Rt△FCD∽ Rt△EAB.于是可得CDDF BEAB=⋅.同理可得CEEG ADAB=⋅.又因为 tanAD BEACBCD CE∠==,所以有 BECD ADCE⋅=⋅,于是可得 DF EG=.解法 2:结论是 DF EG=.下面给出证明 连接 DE,因为90ADB AEB∠=∠= °,所以 A,B,D,E四点共圆,故CED ABC∠=∠.2又 l是⊙O的过点 C 的切线,所以ACGABC∠=∠.所以,CEDACG∠=∠,于是 DE∥FG,故 DF=EG.3、是否存在一个三边长恰是三个连续正整数,且其中一个内角等于另一个内角 2 倍的△ABC?证明你的结论.解:存在满足条件的三角形.当△ABC的三边长分别为6=a,4=b,5=c时,BA∠=∠2.… … … … … …5 分如图,当BA∠=∠2时,延长 BA至点 D,使bACAD==.连接 CD,则△ ACD为等腰三角形.因为BAC∠为△ ACD的一个外角,所以2BACD∠= ∠ .由已知,2BACB∠= ∠ ,所以DB∠=∠.所以△CBD为等腰三角形.又D∠为△ ACD与△CBD的一个公共角,有△ ACD∽△CBD,于是BDCDCDAD =, 即cbaab+=,所以()cbba+=2.而264 (45)= × +,所以此三角形满足题设条件,故存在满足条件的三角...