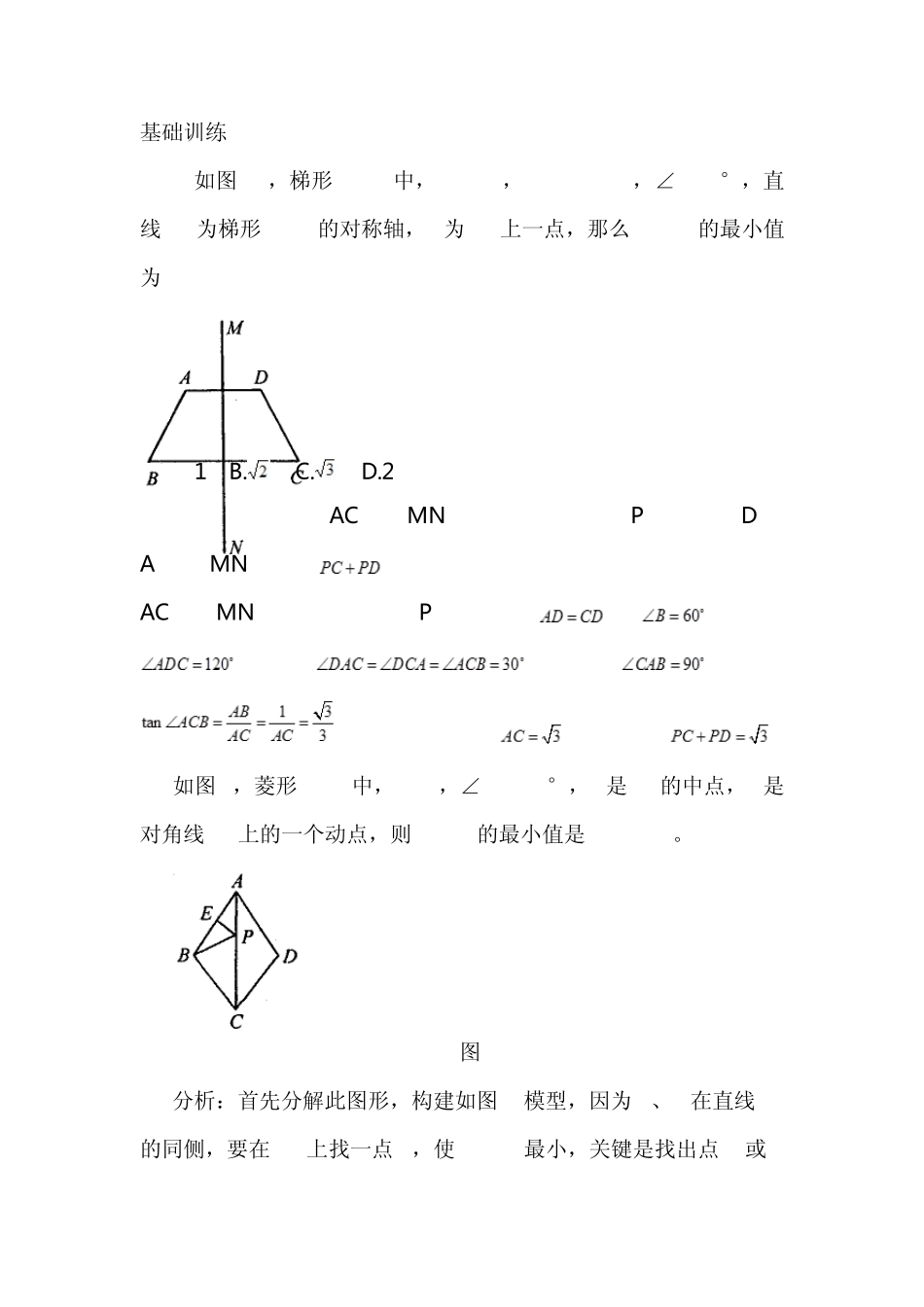
周长最小值专题(完整版 师用) A .线段和最小值 两种基本模型 如图,要在街道旁修建一个奶站P,向居民区A、B 提供牛奶,奶站P 应建在什么地方,才能使从A,B 到它的距离之和最短?为什么? 求线段和最小值的一般步骤: ①选点P 所在直线l为对称轴;画出点A 的对称点A’ ②连结对称点A’与 B 之间的线段,交直线l于点P, 点P 即为所求的点,线段A’B 的长就是 AP+BP 的最小值。 基本解法::利用对称性,将“折”转“直” 基础训练 1.如图11,梯形ABCD中,AD//BC,AB=CD=AD=1,∠B=60°,直线 MN为梯形ABCD的对称轴,P为 MN上一点,那么 PC+PD的最小值为 A.1 B. C. D.2 试题分析:连接 AC,与 MN 所得交点即为所求 P点,因为 D 与A 关于 MN 对称,的最小值即符合两点之间线段最短,所以AC 与 MN 交点即为所求 P 点。因为,,所以,所以,所以,此时,所以,即 2. 如图4,菱形ABCD中,AB=2,∠BAD=60°,E是 AB的中点,P是对角线 AC上的一个动点,则 PE+PB的最小值是________。 图4 分析:首先分解此图形,构建如图5模型,因为 E、B在直线 AC的同侧,要在 AC上找一点 P,使 PE+PB最小,关键是找出点 B或 E关于AC的对称点。如图6,由菱形的对称性可知点B和D关于AC对称,连结DE,此时DE即为PE+PB的最小值, 图5 图6 由∠BAD=60°,AB=AD,AE=BE知, 3223DE 故 PE+PB的最小值为3 。 2.如图,已知点A是半圆上一个三等分点,点B是弧 AN的中点,点P是半径 ON上的动点,若⊙O的半径长为1,则 AP+BP的最小值为___。 P位于A′B与 MN的交点处,AP+BP的值最小; 作 A关于MN的对称点A′,根据圆的对称性,则 A′必在圆上, 连接 BA′交 MN于P,连接 PA,则 PA+PB最小,此时PA+PB=PA′+PB=A′B,连接 OA、OA′、OB, B.三角形周长最小值 1.福建彰州)如图4,∠AOB=45°,P 是∠AOB 内一点,PO=10, (福建彰州)如图4,∠AOB=45°,P 是∠AOB 内一点,PO=10,Q、R 分别是 OA、OB 上的动点,求△PQR 周长的最小值. 分析:点 P 是角内部的一个定点,要在角的两边各确定一点使这三点连成的三角形周长最小,只需将这三边的和转化为以两定点为端点的一条折线. 解:分别作点 P 关于 OA、OB 的对称点 P1、P2,连结 P1P2, 根据轴对称性易知:OP1=OP2=OP=10,∠P1OP2=2∠AOB=90°,因而 P1P2=102, 故△PQR 周长的最小值为102. 2.如图,抛物线y=-x2+b...