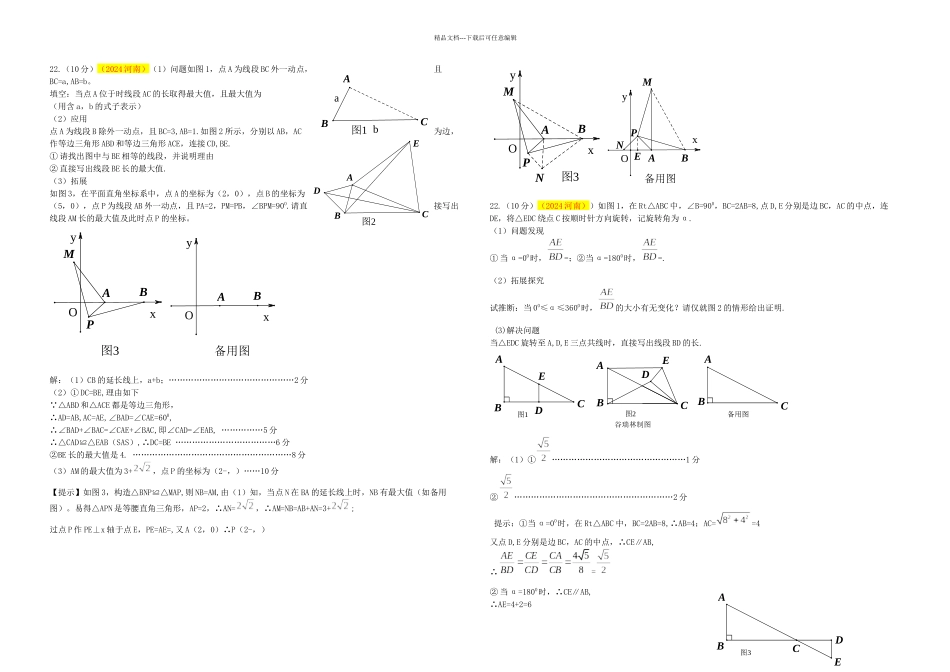
精品文档---下载后可任意编辑22.(10 分)(2024 河南)(1)问题如图 1,点 A 为线段 BC 外一动点,且BC=a,AB=b。填空:当点 A 位于时线段 AC 的长取得最大值,且最大值为(用含 a,b 的式子表示)(2)应用点 A 为线段 B 除外一动点,且 BC=3,AB=1.如图 2 所示,分别以 AB,AC为边,作等边三角形 ABD 和等边三角形 ACE,连接 CD,BE.① 请找出图中与 BE 相等的线段,并说明理由② 直接写出线段 BE 长的最大值. (3)拓展如图 3,在平面直角坐标系中,点 A 的坐标为(2,0),点 B 的坐标为(5,0),点 P 为线段 AB 外一动点,且 PA=2,PM=PB,∠BPM=900.请直接写出线段 AM 长的最大值及此时点 P 的坐标。解:(1)CB 的延长线上,a+b;………………………………………2 分(2)① DC=BE,理由如下 △ABD 和△ACE 都是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=600,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB, ……………5 分∴△CAD≌△EAB(SAS),∴DC=BE ………………………………6 分②BE 长的最大值是 4. …………………………………………………8 分(3)AM 的最大值为 3+,点 P 的坐标为(2-,)……10 分【提示】如图 3,构造△BNP≌△MAP,则 NB=AM,由(1)知,当点 N 在 BA 的延长线上时,NB 有最大值(如备用图)。易得△APN 是等腰直角三角形,AP=2,∴AN=,∴AM=NB=AB+AN=3+;过点 P 作 PE⊥x 轴于点 E,PE=AE=,又 A(2,0)∴P(2-,)22.(10 分)(2024 河南))如图 1,在 Rt△ABC 中,∠B=900,BC=2AB=8,点 D,E 分别是边 BC,AC 的中点,连DE,将△EDC 绕点 C 按顺时针方向旋转,记旋转角为 α.(1)问题发现① 当 α=00时,=;②当 α=1800时,=.(2)拓展探究试推断:当 00≤α≤3600时,的大小有无变化?请仅就图 2 的情形给出证明. (3)解决问题当△EDC 旋转至 A,D,E 三点共线时,直接写出线段 BD 的长.解:(1)①…………………………………………1 分②…………………………………………………2 分 提示:①当 α=00时,在 Rt△ABC 中,BC=2AB=8,∴AB=4;AC==4又点 D,E 分别是边 BC,AC 的中点,∴CE∥AB, ∴=② 当 α=1800时,∴CE∥AB,∴AE=4+2=6图2CBAED图1 baABC图3DEBCA图3OxyPABMyxO备用图AByxO图3PABMNyxO备用图EPABMN谷瑞林制图备用图图2图1EDDEBCCBCBAAAM图 3ABCDENA(D)B(E)C图 1ACBDE图 ...