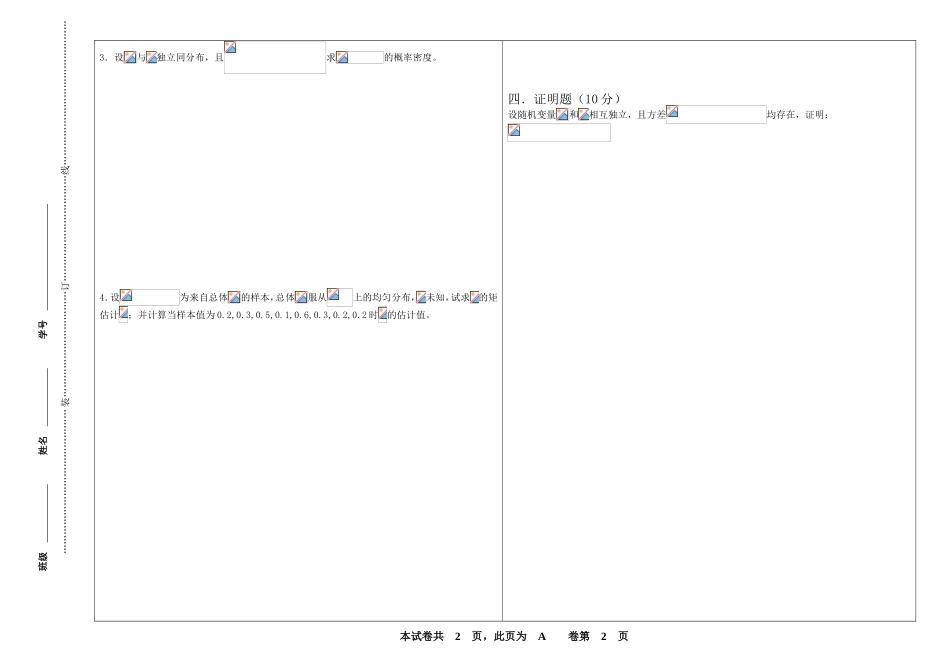
本试卷共2页,此页为A卷第1页(注:参加重修考试者请在重修标识框内打钩)概率统计题号一二三四五六七八九十总分一、选择题(每小题4分,共20分)1.一批产品共10件,其中有2件次品,从这批产品中任取3件,则取出的3件中恰有一件次品的概率为()A.B.C.D.2.设随机变量,,则事件{1}的概率为()A.0.1385B.0.2413C.0.2934D.0.34133.设随机变量与相互独立,且,则()A.B.C.D.4.设,服从参数为的指数分布,则下列各式错误的是()A.B.C.D.5.设为独立同分布的随机变量序列,且都服从参数为的指数分布,则当n充分大时,随机变量的概率分布近似服从()A.B.C.D.二、填空题(每小题4分,共20分)1.设事件相互独立,则___________2.在区间内随机投点,以表示投点的坐标,则的密度函数为:3.若独立且分布函数分别为:,则的分布函数为:4.设随机变量满足:,由切比雪夫不等式估计___.5.设总体服从参数为的泊松分布,其中为未知参数.为来自该总体的一个样样本,则参数的矩估计量为___________.三、计算题(1、2题各10分,3、4题各15分,共50分)1.有三个形状相同的罐,在第一个罐中有2个白球和1个黑球;在第二个罐中有3个白球和1个黑球;在第三个罐中有2个白球和2个黑球;某人随机地选取一罐,再从该罐中选取一球,试问这球是白球的概率有多大?2.设随机变量具有概率密度函数.试求:(1)常数;(2)A卷班级姓名学号………………………………………装……………………………订……………………………线………………………………………本试卷共2页,此页为A卷第2页3.设与独立同分布,且求的概率密度。4.设为来自总体的样本,总体服从上的均匀分布,未知,试求的矩估计;并计算当样本值为0.2,0.3,0.5,0.1,0.6,0.3,0.2,0.2时的估计值。四.证明题(10分)设随机变量和相互独立,且方差均存在,证明:班级姓名学号………………………………………装……………………………订……………………………线………………………………………本试卷答案共1页,此页为第1页