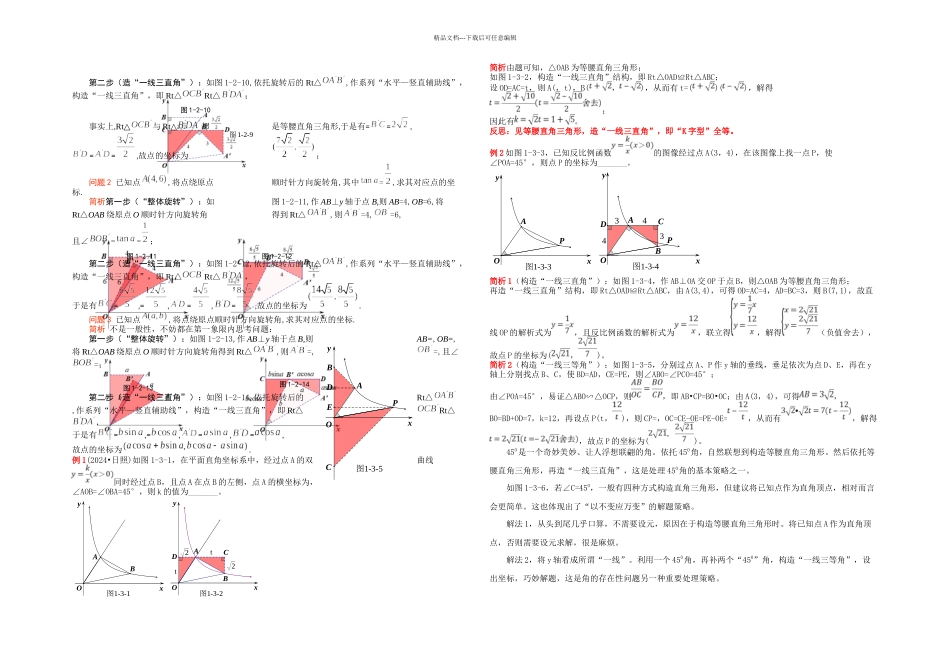
yx3344A'E'AEOαααDEDECAACBB精品文档---下载后可任意编辑第 1 讲角的存在性处理策略 知识必备一、一线三等角 1.如图 1-1-1,且,此为“一线三直角”全等,又称“K 字型”全等; 图 1-1-1 图 1-1-2 图 1-1-3 图 1-1-42.如图 1-1-2,,此为“一线三直角”相似,又称“K 字型”相似;3.如图 1-1-3,,此为更一般的“一线三等角”.二、相似三角形的性质 相似三角形的对应边成比例,其比值称为相似比; 相似三角形的对应线段成比例.三、正切的定义 如图 1-1-4,在中,,即的正切值等于的对边与的邻边之比;同理,,则,即互余两角的正切值互为倒数.方法提炼一、基本策略:联想构造二、构造路线方式(一):构造“一线三等角”o角构等腰直角三角形造“一线三直角”全等,如图 1-2-1; 图 1-2-1o角构直角三角形造“一线三直角”相似,如图 1-2-2; 图 1-2-23.tanα=k→构直角三角形→造“一线三直角”相似,如图 1-2-3;4.“一线三等角”的应用分三重境界;一重境:当一条线上已有三个等角时,只要识别、证明,直接应用模型解题,如图 1-2-4 所示的“同侧型一线三等角”及图 1-2-5 所示的“异侧型一线三等角”;二重境:当一条线上已有两个等角时,需要再补上一个等角,构造模型解题;三重境:当一条线上只有一个角时,需要再补上两个等角,构造模型解题,如图 1-2-6 及图 1-2-7 所示;方式(二):构造“母子型相似”“角处理”,还可以在角的一边上某点处作水平或竖直辅助线,造成某水平边或竖直边对此角结构,然后在这条线上补出一个与此角相等的角,构造出“母子型相似”,其核心结构如图 1-2-8 所示.方式(三):整体旋转法(*)前两种构造属静态构造方式,再介绍一种动态构造方式,即整体旋转法,其核心思想是“图形的旋转(运动)本质是图形上点旋转(运动);反过来,点的旋转(运动)可以看成该点所在图形的旋转(运动)”.下面以三个问题说明此法:问题 1 已知点 A(3,4),将点 A 绕原点 O 顺时针方向旋转 45º 角,求其对应点 A’的坐标.简析 第一步 (“整体旋转”):如图 1-2-9,作 AB⊥y 轴于点 B,则AB=3,OB=4,点 A 绕原点 O 顺时针方向旋转 45º 得到点 A’,可看成 Rt△OAB 绕原点 O 顺时针方向旋转45º 得到 Rt△OA’B‘,则 A’B’=8,OB’=4,且∠BOB’=45º; DAC DEA→DA2=DC∙DE→DG2+AG2=DC∙DE动动定定定定定定定定定GACBBCAACBDDE图 1-2-3图 1-...