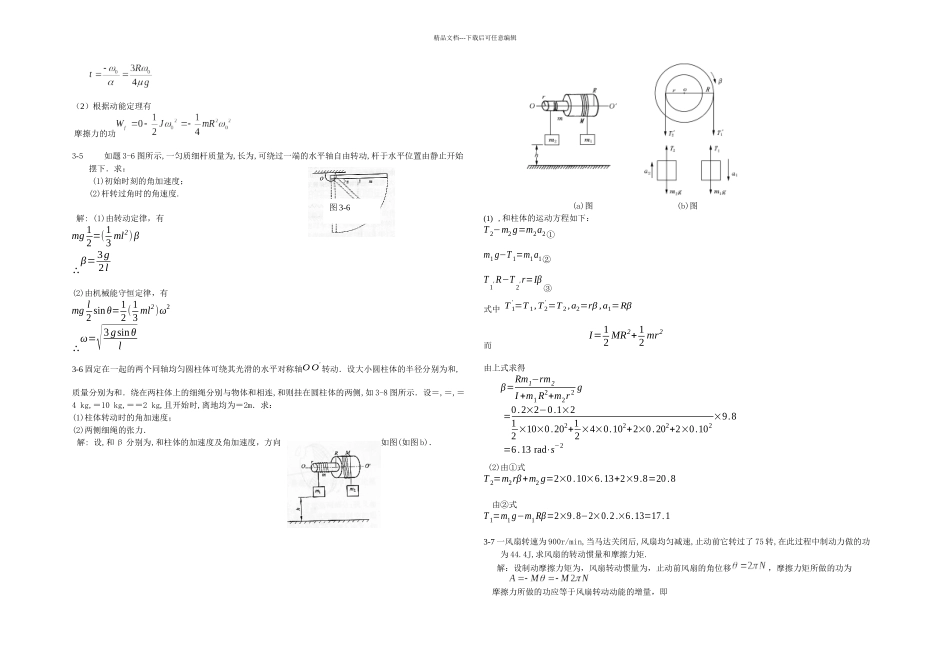
精品文档---下载后可任意编辑3-1 如图 3-1 示,一轻杆长度为,两端各固定一小球,A 球质量为,B 球质量为,杆可绕过中心的水平轴 O 在铅垂面内自由转动,求杆与竖直方向成角时的角加速度. 解:系统受外力有三个,即 A,B 受到的重力和轴的支撑作用力,轴的作用力对轴的力臂为零,故力矩为零,系统只受两个重力矩作用. 以顺时针方向作为运动的正方向,则 A 球受力矩为正,B 球受力矩为负,两个重力的力臂相等为,故合力矩为 系统的转动惯量为两个小球(可视为质点)的转动惯量之和应用转动定律 有:解得 3-2 计算题 3-2 图所示系统中物体的加速度.设滑轮为质量均匀分布的圆柱体,其质量为,半径为,在绳与轮边缘的摩擦力作用下旋转,忽略桌面与物体间的摩擦,设=50kg,=200kg,M=15kg,=.解: 分别以,滑轮为讨论对象,受力图如图(b)所示.对 ,运用牛顿定律,有m2 g−T 2=m2a ①T 1=m1 a②对滑轮运用转动定律,有T 2r−T 1r=( 12 Mr2)β③又,a=rβ ④联立以上 4 个方程,得a=m2 gm1+m2+ M2=200×9.85+200+152=7.6m⋅s−23-3 飞轮质量为 60kg,半径为,当转速为 1000r/min 时,要在 5s 内令其制动,求制动力,设闸瓦与飞轮间摩擦系数=0.4,飞轮的转动惯量可按匀质圆盘计算,闸杆尺寸如图所示. 解:以飞轮为讨论对象,飞轮的转动惯量,制动前角速度为rad/s,制动时角加速度为- 制动时闸瓦对飞轮的压力为,闸瓦与飞轮间的摩擦力,运用转动定律,得则 以闸杆为讨论对象,在制动力和飞轮对闸瓦的压力的力矩作用下闸杆保持平衡,两力矩的作用力臂分别为m 和=0-50m,则有N3-4 设有一均匀圆盘,质量为,半径为,可绕过盘中心的光滑竖直轴在水平桌面上转动. 圆盘与桌面间的滑动摩擦系数为,若用外力推动它使其角速度达到时,撤去外力,求:(1) 此后圆盘还能继续转动多少时间?(2) 上述过程中摩擦力矩所做的功.解:(1)撤去外力后,盘在摩擦力矩作用下停止转动- 设盘质量密度为,则有根据转动定律 图 3-1图 3-2图 3-3精品文档---下载后可任意编辑(2)根据动能定理有 摩擦力的功3-5 如题 3-6 图所示,一匀质细杆质量为,长为,可绕过一端的水平轴自由转动,杆于水平位置由静止开始摆下.求:(1)初始时刻的角加速度;(2)杆转过角时的角速度.解: (1)由转动定律,有mg 12=( 13 ml2) β∴β=3g2l(2)由机械能守恒定律,有mg l2 sinθ=12 ( 13 ml2)ω2∴ω=√3 gsinθl3-6 固定在一起的两个同轴均匀圆柱体可绕其光滑...