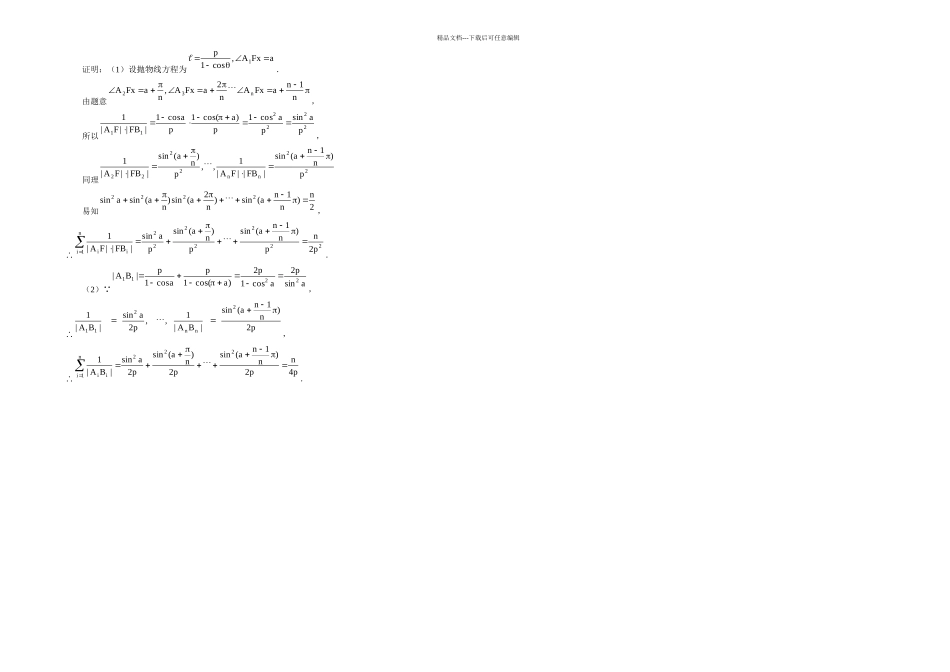
精品文档---下载后可任意编辑过抛物线y2=2 px (p>0)的焦点 F 作一条直线 L 和此抛物线相交于 A( x1, y1)、B( x2, y2)两点结论 1:|AB|=x1+ x2+p|AB|=|AF|+|BF|=( x1+ p2 )+( x2+ p2 )=x1+x2+ p结论 2:若直线 L 的倾斜角为,则弦长|AB|= 2 psin2θ证: (1)若θ= π2 时,直线 L 的斜率不存在,此时 AB 为抛物线的通径,∴|AB|=2 p∴结论得证(2)若θ≠ π2 时,设直线 L 的方程为:y=( x− p2 )tan θ即x=y⋅cotθ+ p2 代入抛物线方程得y2−2 py⋅cotθ−p2=0 由韦达定理y1 y2=−p2, y1+ y2=2 pcot θ由弦长公式得|AB|=√1+cot2θ|y1−y2|=2 p(1+cot2θ)= 2 psin2θ结论 3: 过焦点的弦中通径长最小 sin2θ≤1∴ 2 psin2θ≥2 p|AB|的最小值为,即过焦点的弦长中通径长最短.结论 4:S2Δ oAB|AB| = p38 (为定值)SΔOAB=S ΔOBF+S Δ0 AF=12 |OF|⋅|BF|⋅sinθ+12|OF|⋅|AF|⋅sinϑ¿12 |OF|⋅(|AF|+|BF|)sinθ=12 |OF|⋅|AB|⋅sinθ=12⋅p2 ⋅2 psin2θ⋅sinθ=p22sinθ∴S ΔOAB2|AB| =P38结论 5: (1) y1 y2=−p2 (2) x1x2=p24证 x1=y122 p ,x2=y222 p ,∴ x1 x2=( y1 y2)24 P2= P24结论 6:以 AB 为直径的圆与抛物线的准线相切 证:设 M 为 AB 的中点,过 A 点作准线的垂线 AA1, 过 B 点作准线的垂线 BB1, 过 M 点作准线的垂线 MM1,由梯形的中位线性质和抛物线的定义知|MM 1|=|AA1|+|BB1|2=|AF|+|BF|2=|AB|2 故结论得证 结论 7:连接 A1F、B1 F 则 A1FB1F AA1=AF,∴∠ AA1F =∠ AFA1 AA1 //OF ∴∠ AA1F =∠ A1FO ∴∠ A1FO =∠ A1FA同理∠B1 FO =∠B 1 FB∴∠ A1FB1=90° A1FB1 F结论 8:(1)AM1BM1 (2)M1FAB (3)|M1 F|2=|AF|⋅|BF|(4)设 AM1 与 A1F 相交于 H ,M1B 与 FB1相交于 Q 则 M1,Q,F ,H 四点共圆(5)|AM 1|2+|M1B|2=4|M1 M|2证:由结论(6)知 M1 在以 AB 为直径的圆上 AM1BM1ΔA1 FB1为直角三角形, M1 是斜边 A1 B1 的中点 ∴ A1 M1=M1 F∴∠ M1FA1=∠M1 A1F ∠ AA1 F=∠ AFA1 ∠ AA1 F+∠ FA1 M 1=∠ AA1 M 1=90° ∴∠ AFA1+∠ A1 FM 1=90°M1FAB∴|M1F|2=|AF|⋅|BF| AM1BM1 ∴∠ AM 1 B=90° 又 A1 F⊥B1 F∴∠ A1FB1=90° 所以 M1,Q,F,H 四点共圆,|AM 1|2+|M1B|2=|AB|2=(|AF|+|BF|)2=(...