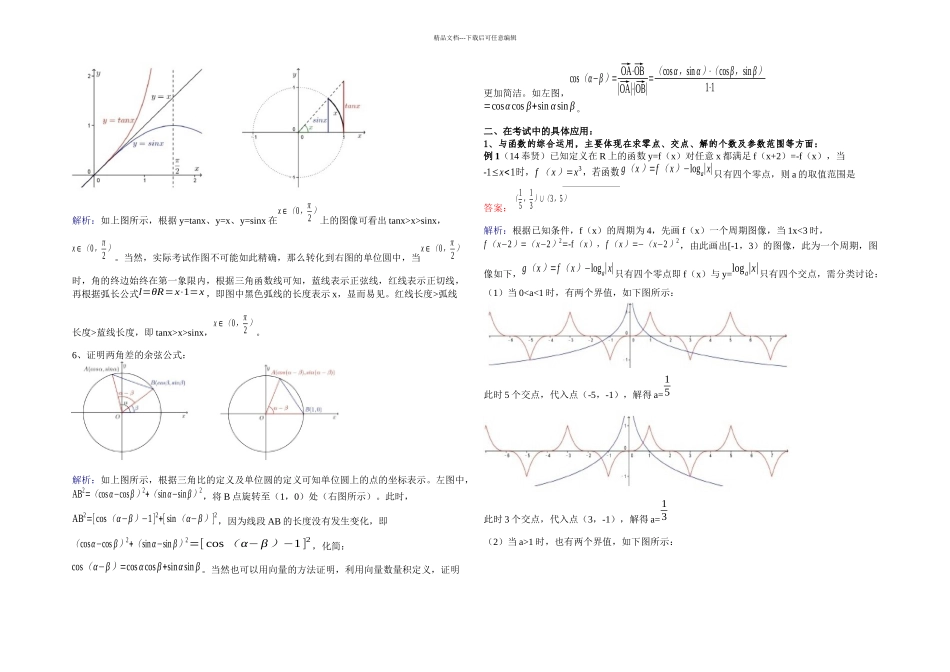
精品文档---下载后可任意编辑一、在一些命题证明中的应用举例:1、证明勾股定理:4×(0.5ab)+(a−b)2=a2+b2=c2解析:上图中,四个小三角形(阴影部分)的面积加上中间小正方形的面积等于大正方形的面积,化简后得到勾股定理a2+b2=c2 。2、证明乘法公式(平方差与完全平方):a2−b2=(a+b)(a−b)(a+b)2=a2+b2+2ab解析:在上图中,利用正方形和小正方形面积的转化,能更进一步理解平方差公式与完全平方公式的运算过程以及公式的本质问题。3、证明基本不等式:解析:如上图所示,直角三角形斜边上的中线等于斜边的一半,长度为a+b2,根据直角三角形的相似关系,可以得到直角三角形斜边上的高的长度为√ab,显然在直角三角形中,斜边上的中线的长度会大于等于高,利用这样简洁明了的几何图解,对基本不等式的理解也就更加简单了。4、证明正(余)弦定理:解析:(1)如上图所示,Δ ABC的面积S=12 a⋅h=12 a⋅bsinC⇒bsinC=csinB;即bsinB =csinC ,同理可得asinA = bsinB = csinC ;根据圆的性质(等弧对等角)∠ A=∠ D,sinA=sinD= a2R ,即asinA =2R;综上,得正弦定理:asinA = bsinB = csinC =2R。(2)根据勾股定理AB2−BE2=AC2−CE2,即c2−(c⋅cosB)2=b2−(a−c⋅cosB)2;整理可得余弦定理:cosB=a2+c2−b22ac;同理得出 cosA、cosC 的余弦定理。5、证明结论tanx>x>sinx, x∈(0, π2 )精品文档---下载后可任意编辑解析:如上图所示,根据 y=tanx、y=x、y=sinx 在x∈(0,π2)上的图像可看出 tanx>x>sinx,x∈(0,π2)。当然,实际考试作图不可能如此精确,那么转化到右图的单位圆中,当x∈(0,π2)时,角的终边始终在第一象限内,根据三角函数线可知,蓝线表示正弦线,红线表示正切线,再根据弧长公式l=θR=x⋅1=x ,即图中黑色弧线的长度表示 x,显而易见。红线长度>弧线长度>蓝线长度,即 tanx>x>sinx,x∈(0,π2)。6、证明两角差的余弦公式:解析:如上图所示,根据三角比的定义及单位圆的定义可知单位圆上的点的坐标表示。左图中,AB2=(cosα−cosβ )2+(sinα−sin β)2,将 B 点旋转至(1,0)处(右图所示)。此时,AB2=[cos(α−β)−1]2+[sin(α−β)]2,因为线段 AB 的长度没有发生变化,即(cosα−cos β)2+(sinα−sin β)2=[ cos(α− β)−1]2 ,化简:cos(α−β )=cosαcosβ+sinαsin β。当然也可以用向量的方法证明,利用向量数...