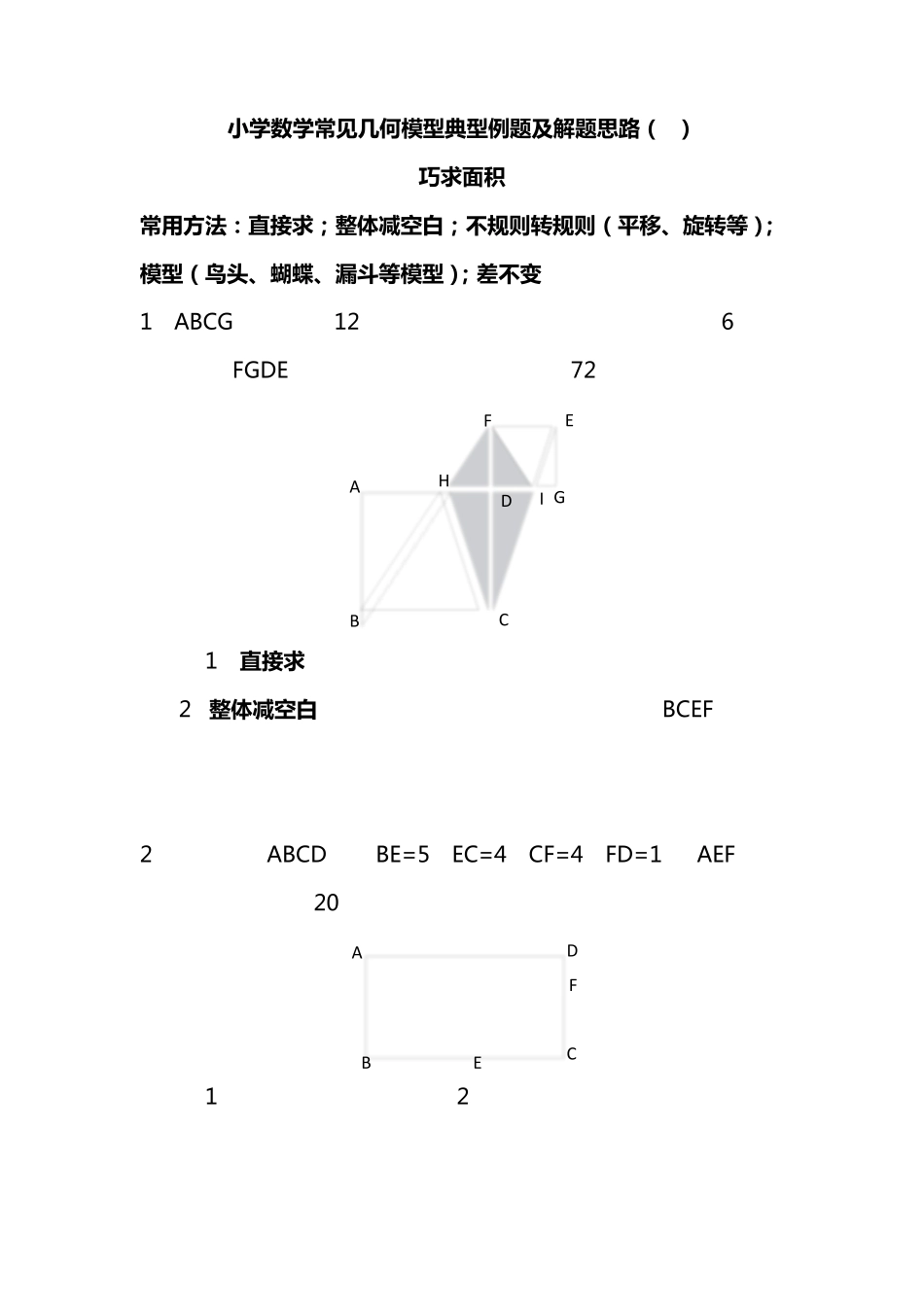
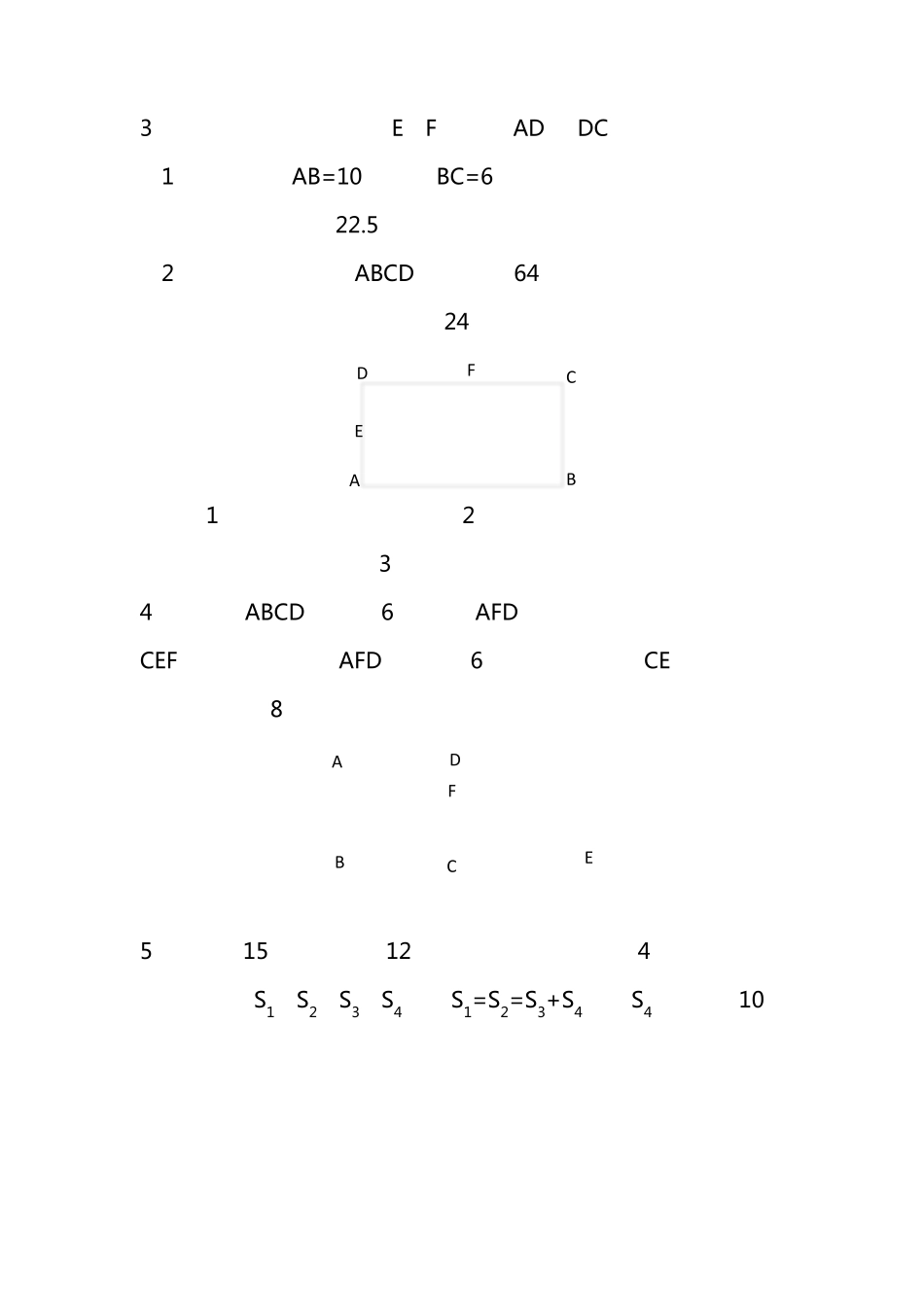
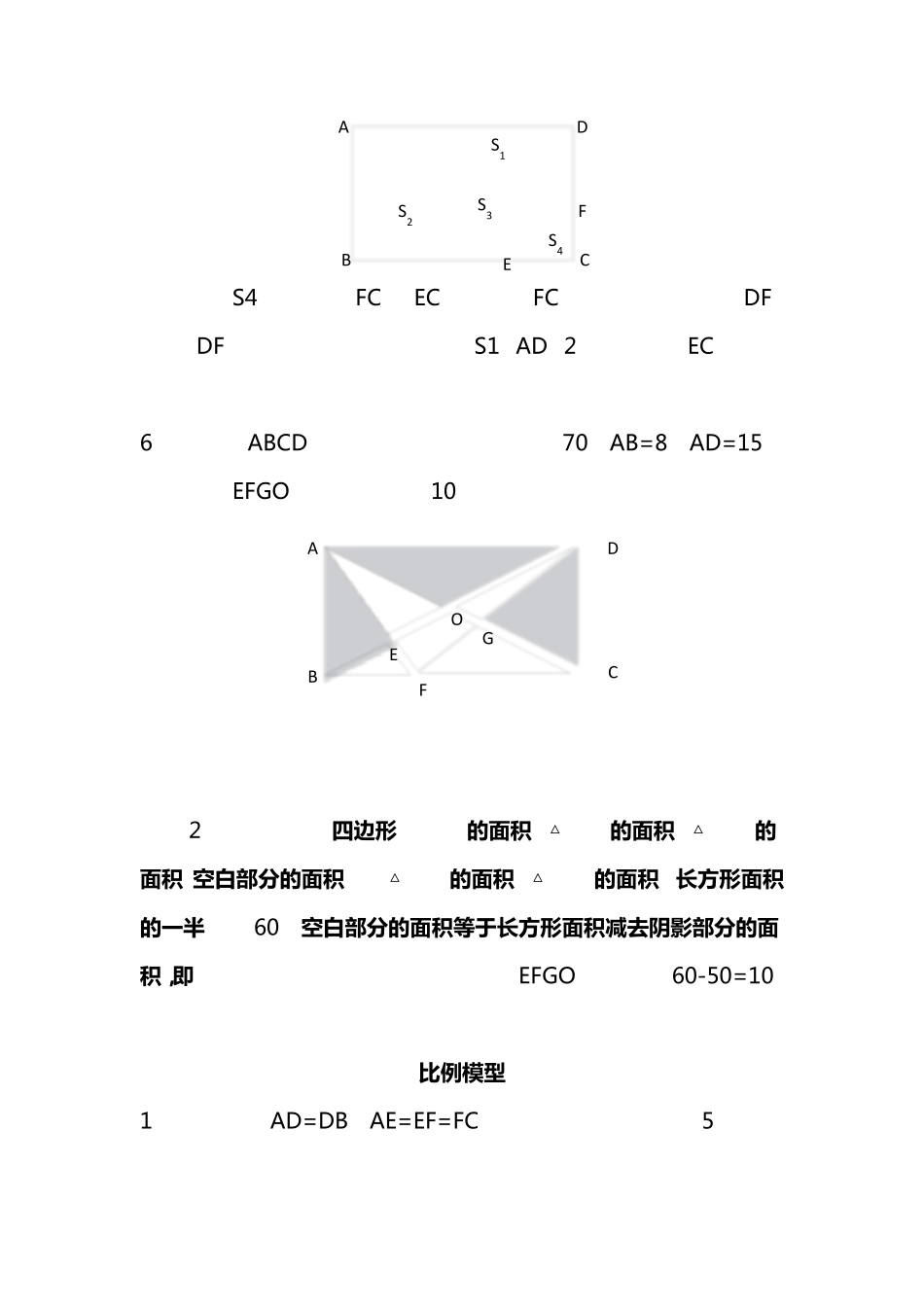
小 学 数 学 常 见 几 何 模 型 典 型 例 题 及 解 题 思 路 ( 1) 巧 求 面 积 常 用 方 法 : 直 接 求 ; 整 体 减 空 白 ; 不 规 则 转 规 则 ( 平 移 、旋转 等);模 型 ( 鸟头、蝴蝶、漏斗等模 型 ); 差不 变 1、ABCG 是边长为 12 厘米的正方形,右上角是一个边长为 6 厘米的正方形 FG DE,求阴影部分的面积。答案:72 AHFECBIDG 思路:1)直 接 求 ,但是阴影部分的三角形和四边形面积都无法直接求;2)整 体 减 空 白 。关键在于如何找到整体,发现梯形 BCEF 可求,且空白分别两个矩形面积的一半。 2、在长方形 ABCD 中,BE=5,EC=4,CF=4,FD=1。△AEF 的面积是多少?答案:20 ADBFCE 思路:1)直接求,无法直接求;2)由于知道了各个边的数据,因此空白部分的面积都可求 3、如图所示的长方形中,E、F 分别是 AD 和 DC 的中点。 (1)如果已知 AB=10 厘米,BC=6 厘米,那么阴影部分面积是多少平方厘米?答案:22.5 (2)如果已知长方形 ABCD 的面积是 64 平方厘米,那么阴影部分的面积是多少平方厘米?答案:24 ABCDFE 思路(1)直接求,无法直接求;2)已经知道了各个边的数据,因此可以求出空白的位置;3)也可以利用鸟头模型 4、正方形 ABCD 边长是 6 厘米,△AFD(甲)是正方形的一部分,△CEF(乙)的面积比△AFD(甲)大 6 平方厘米。请问 CE 的长是多少厘米。答案:8 ABEDCF 思路:差不变 5、把长为 15 厘米,宽为 12 厘米的长方形,分割成 4 个三角形,其面积分别为 S1、S2、S3、S4,且 S1=S2=S3+S4。求 S4。答案:10 ADBCEFS1S2S3S4 思路:求 S4 需要知道 FC 和 EC 的长度;FC 不能直接求,但是 DF可求,DF 可以由三分之一矩形面积 S1÷AD×2 得到,同理 EC 也求。最后一句三角形面积公式得到结果。 6、长方形 ABCD 内的阴影部分面积之和为 70,AB=8,AD=15。求四边形 EFGO 的面积。答案 10。 ABCDFOEG 思路:看到长方形和平行四边形,只要有对角线,就知道里面四个三角形面积相等。然后依据常规思路可以得到答案。 思路 2:从整体看,四 边 形 EFGO的 面 积 =△AFC的 面 积 +△BFD的面 积 -空 白 部 分 的 面 积 。而△ACF的 面 积 +△BFD的 面 积 =长 方 形 面 积的 一半,即 60。空 白 部 分 的 面 积 等于长 方 形 ...