微专题平面向量中最值问题归纳

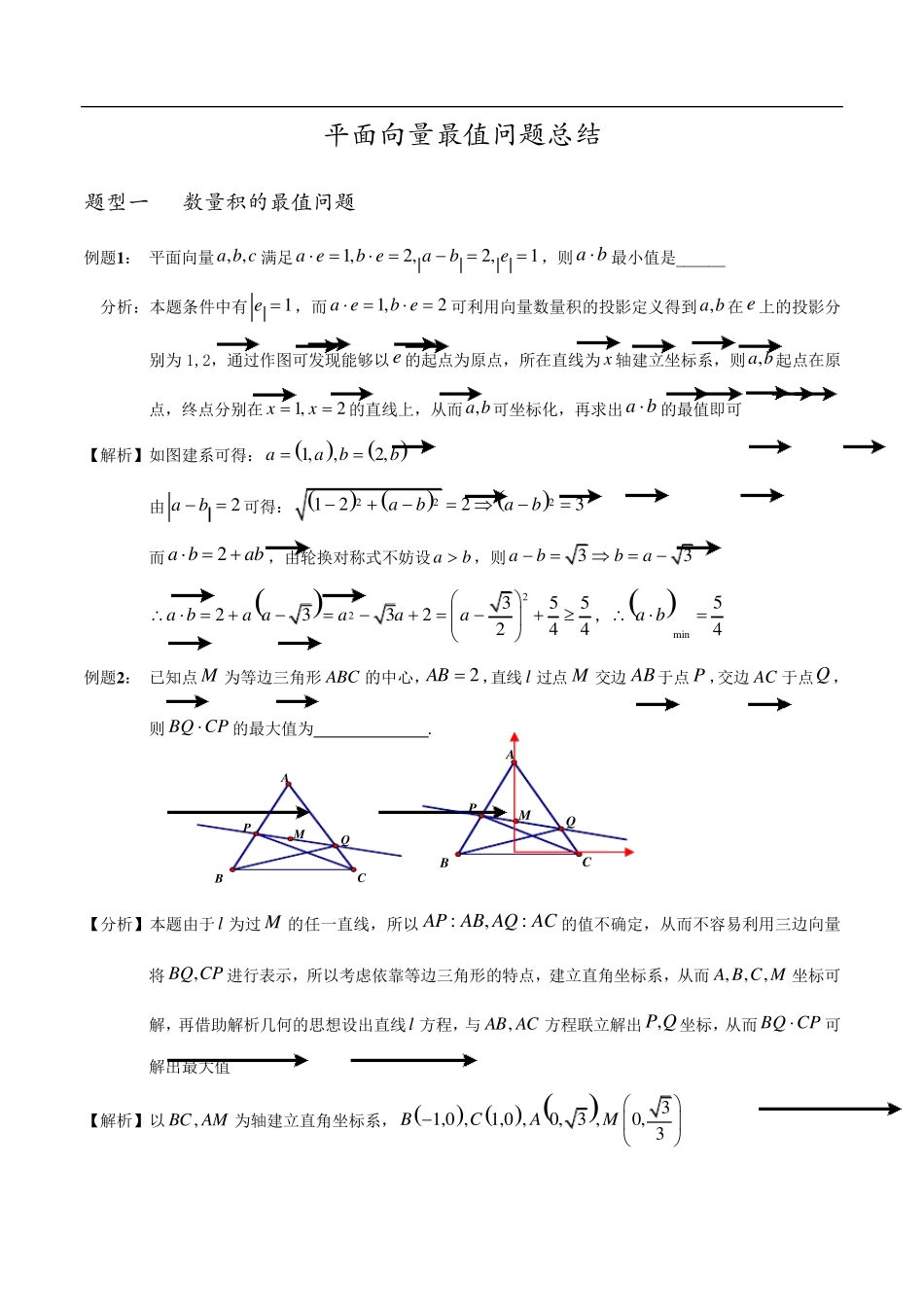
平 面 向 量 最 值 问 题 总 结 题 型 一 数 量 积 的 最 值 问 题 例题1： 平面向量, ,a b c 满足1,2,2,1a eb eabe，则a b最小值是_ _ _ _ _ _ 分析：本题条件中有1e ，而1,2a eb e可利用向量数量积的投影定义得到,a b 在e 上的投影分别为1,2，通过作图可发现能够以e 的起点为原点，所在直线为x 轴建立坐标系，则,a b起点在原点，终点分别在1,2xx的直线上，从而,a b可坐标化，再求出a b的最值即可 【解析】如图建系可得：1,,2,aabb 由2ab可得：2221223abab 而 2a bab，由轮换对称式不妨设ab，则33abba 223552332244a ba aaaa ，min54a b 例题2： 已知点M 为等边三角形 ABC 的中心，2AB ，直线l 过点M 交边 AB于点P ，交边 AC 于点Q ， 则BQ CP的最大值为 . 【分析】本题由于l 为过M 的任一直线，所以:,:AP AB AQ AC 的值不确定，从而不容易利用三边向量将,BQ CP 进行表示，所以考虑依靠等边三角形的特点，建立直角坐标系，从而,,,A B C M 坐标可解，再借助解析几何的思想设出直线l 方程，与,AB AC 方程联立解出,P Q 坐标，从而BQ CP可解出最大值 【解析】以,BC AM 为轴建立直角坐标系， 31,0 ,1,0 ,0, 3 ,0, 3BCAM  QPABCMQPABCM 设直线3:3lykx，由 1,0 ,1,0 ,0, 3BCA可得： :31 ,:31AByxACyyx  3:331ykxPyx得： 2 333313xkkyk；3:331ykxQyx 得： 2 333313xkkyk 5 33315 3331,,,333333kkkkBQCPkkkk  2222225 335 3331317593162239333333333kkkkkkkBQ CPkkkkkkk 222226221 618401406333333kkkkk 例题3： 已知圆C 的方程22(1)1xy，P是椭圆22143xy上一点，过P作圆的两条切线，切点为A， B，则PA PB的取值范围为（ ） A．3[ ,)2  B．[2 23,) C．562 23...