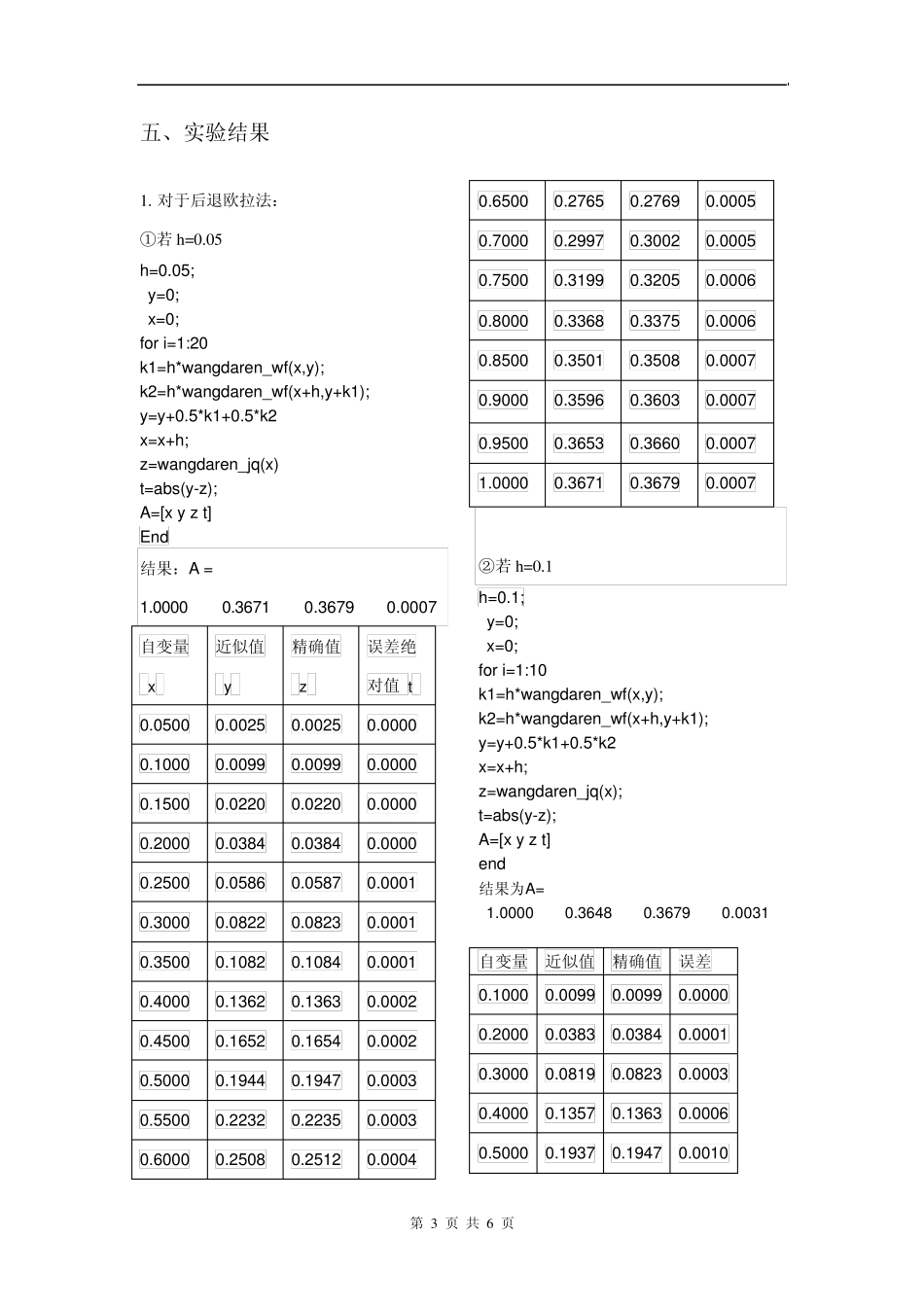
第 1 页 共 6 页 数值计算方法实验上机测验 微分方程求解的后退欧拉法、龙格库塔法(三阶、四阶) 日期: 2011-06-16 一、测验目的 1. 学习matlab 的使用方法。 2. 掌握常微分方程的几种数值解法:后退欧拉法、龙格库塔法(三阶、四阶)。 3. 比较各方法的数值解及误差,了解各方法的优缺点。 二、实验题目 给定的初值问题 0,0)1(222yxeyexdxdyxx 及其精确解22xexy 按 (1)后退欧拉法,步长h=0.05, h=0.1; (2)三阶龙格—库塔法,步长h=0.05, h=0.1; (3)四阶标准龙格—库塔法,步长h=0.05,h=0.1; 求在节点10.1 (1,2,,10)kxk k 处的数值解及误差比较各方法的优缺点。 三、实验原理 1.对于后退欧拉法: 利用 ( 0 )1(1 )111(,)(,)nnnnknnnnyyh fxyyyh fxy进行迭代求解可以完成计算 需要将微分方程表达式和精度计算表达式作为两个函数保存在 m 文件里并在程序中调用: 第 2 页 共 6 页 ①微分方程(wangdaren_wf) function z=wangdaren(x,y) z=-2*x*(y*exp(x^2)-1)/exp(x^2) end ②精确解计算(wangdaren _jq) function z= wangdaren _jq(x) z=x*x/exp(x^2) end 龙格—库塔法基本思想: 用( , )f x y 在几个不同点的数值加权平均斜率[, ()]nnKf xh y xh ,使截断误差的阶数尽可能高。即取不同点的斜率的加权平均作为平均斜率,以便提高阶数。 2.对于三阶龙格—库塔法: 利用1123121312(4)6(,)11(,)22(,2)nnnnnnnnhyykkkkf xykf xh yhkkf xh yhkhk 可以完成计算 3.对于四阶龙格—库塔法: 利用),()3,32()3,3(),()33(8321421312143211hkhkhkyhxfkhkkhyhxfkkhyhxfkyxfkkkkkhyynnnnnnnnnn 可以完成计算 四、实验内容 由上述实验原理叙述的后退欧拉法,三阶龙格—库塔法,四阶龙格—库塔法几种常微分方程数值解法分别对已给定的初值问题进行求解,比较各方法的数值解及误差,了解各方法的优缺点。 第 3 页 共 6 页 五、实验结果 1. 对于后退欧拉法: ①若 h=0.05 h=0.05; y=0; x=0; for i=1:20 k1=h*wangdaren_wf(x,y); k2=h*wangdaren_wf(x+h,y+k1); y=y+0.5*k1+0.5*k2 x=x+h; z=wangdaren_jq(x) t=abs(y-z); A=[x y z t] End 结果:A =...