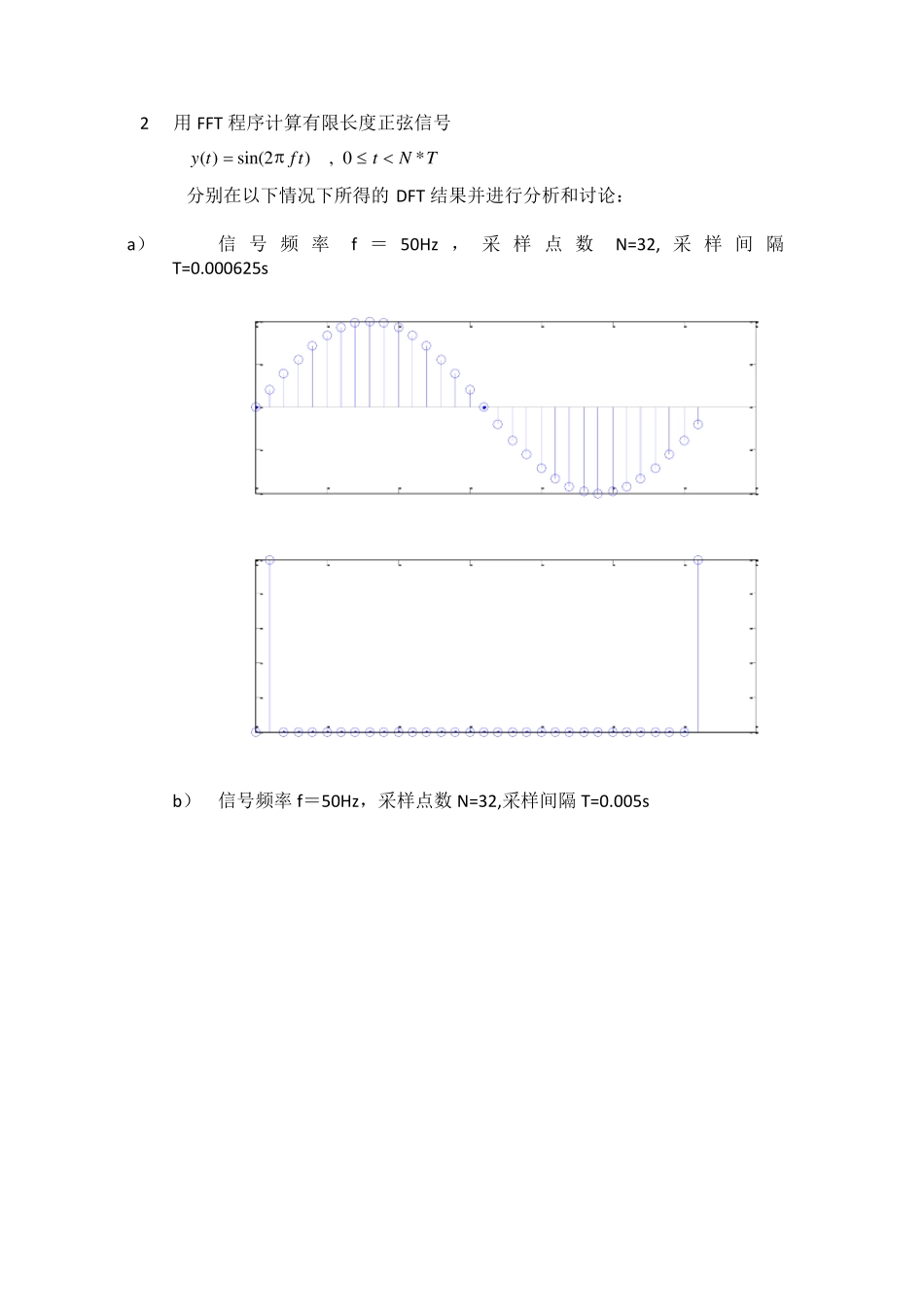
一、实验目的 1 在理论学习的基础上,通过本实验加深对快速傅立叶变换的理解; 2 熟悉并掌握按时间抽取FFT算法的程序; 3 了解应用FFT进行信号频谱分析过程中可能出现的问题,例如混淆、泄漏、栅栏效应等,以便在实际中正确应用FFT。 二、实验内容 1 仔细分析教材第六章‘时间抽取法FFT ’的算法结构,编制出相应的用FFT进行信号分析的C 语言(或 MATLAB 语言)程序; 用MATLAB 语言编写的FFT源程序如下: %% 输入数据f、N、T及是否补零 clc; clear; f=input(' 输入信号频率 f:'); N=input(' 输入采样点数 N:'); T=input(' 输入采样间隔 T:'); C=input(' 信号是否补零(补零输入 1,不补零输入 0):'); %补零则输入 1,不补则输入 0 if(C==0) t=0:T:(N-1)*T; x=sin(2*pi*f*t); b=0; else b=input('输入补零的个数: '); while(log2(N+b)~=fix(log2(N+b))) b=input('输入错误,请重新输入补零的个数: '); end t=0:T:(N+b-1)*T; x=sin(2*pi*f*t).*(t<=(N-1)*T); end %% fft算法的实现 A=bitrevorder(x); % 将序列按二进制倒序 N=N+b; M=log2(N); % M为蝶形算法的层数 W=exp(-j*2*pi/N); for L=1:1:M % 第L层蝶形算法 B=2^L/2; % B为每层蝶形算法进行加减运算的两个数的间隔 K=N/(2^L); % K为每层蝶形算法中独立模块的个数 for k=0:1:K-1 for J=0:1:B-1 p=J*2^(M-L); % p是W的指数 q=A(k*2^L+J+1); % 用q来代替运算前面那个数 A(k*2^L+J+1)=q+W^p*A(k*2^L+J+B+1); A(k*2^L+J+B+1)=q-W^p*A(k*2^L+J+B+1); end end end %% 画模特性的频谱图 z=abs(A); % 取模 z=z./max(z); %归一化 hold on subplot(2,1,1); stem(0:1:N-1,x,'DisplayName','z'); title(' 时域信号 '); subplot(2,1,2); stem(0:1:N-1,z,'DisplayName','z'); title('频谱图'); figure(gcf) %画图 2 用FFT 程序计算有限长度正弦信号 ( )sin(2), 0*y tfttNT 分别在以下情况下所得的 DFT 结果并进行分析和讨论: a) 信号频 率f = 50Hz , 采 样 点 数N=32, 采 样 间 隔T=0.000625s05101520253035-1-0.500.510510152025303500.20.40.60.81 b) 信号频率 f=50Hz,采样点数 N=32,采样间隔 T=0.005s 05101520253035-1-0.500.510510152025303500.20.40.60.81 c) 信号频率 f=50Hz,采样点数 N=32,采样间隔 T=0.0046875s 0510152025...