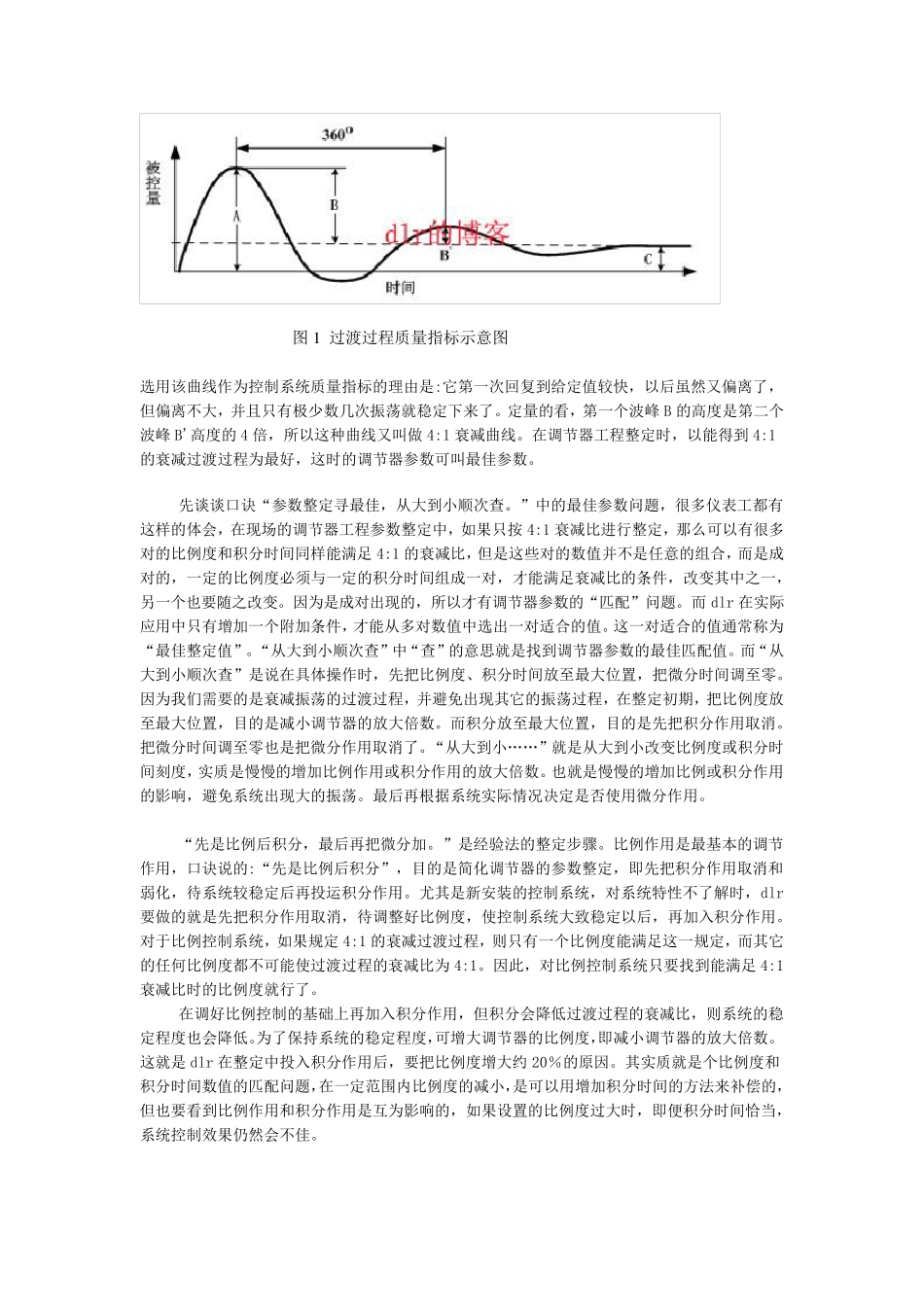
我们先看网上流传的 PID 参数整定口诀: 参数整定找最佳,从小到大顺序查 先是比例后积分,最后再把微分加 曲线振荡很频繁,比例度盘要放大 曲线漂浮绕大湾,比例度盘往小扳 曲线偏离回复慢,积分时间往下降 曲线波动周期长,积分时间再加长 曲线振荡频率快,先把微分降下来 动差大来波动慢。微分时间应加长 理想曲线两个波,前高后低 4 比 1 一看二调多分析,调节质量不会低。 它是什么时候开始在网上流传的不太清楚。 现在再看另一首口诀: 参数整定寻最佳,从大到小顺次查。 先是比例后积分,最后再把微分加。 曲线振荡很频繁,比例度盘要放大。 曲线漂浮绕大弯,比例度盘往小扳。 曲线偏离回复慢,积分时间往下降。 曲线波动周期长,积分时间再加长。 理想曲线两个波,调节过程高质量。 这是一首用经验法进行 PID 参数工程整定的口诀,该口诀流传至今已有几十年了,其最早出现在 1973 年 11 月出版的《化工自动化》一书中。现在网上流传的口诀,看来大多是以该口诀作为蓝本进行了补充和改编而来的,如:“ 曲线振荡频率快,先把微分降下来,动差大来波动慢。微分时间应加长。”还有的加了:“ 理想曲线两个波,前高后低 4 比 1,一看二调多分析,调节质量不会低。”等等。 现 dlr 结合这两首口诀,进行一些浅析。 控制系统在设计、整定和运行中,衡量系统质量的依据就是系统的过渡过程。当系统的输入为阶跃变化时,系统的过渡过程表现有:发散振荡、等幅振荡、衰减振荡、单调过程等形式。在多数情况下,dlr 都希望得到衰减振荡的过渡过程,且认为如图1 所示的过渡过程最好,并把它作为衡量控制系统质量的依据。 图1 过渡过程质量指标示意图 选用该曲线作为控制系统质量指标的理由是:它第一次回复到给定值较快,以后虽然又偏离了,但偏离不大,并且只有极少数几次振荡就稳定下来了。定量的看,第一个波峰B 的高度是第二个波峰B'高度的4 倍,所以这种曲线又叫做4:1 衰减曲线。在调节器工程整定时,以能得到4:1的衰减过渡过程为最好,这时的调节器参数可叫最佳参数。 先谈谈口诀“参数整定寻最佳,从大到小顺次查。”中的最佳参数问题,很多仪表工都有这样的体会,在现场的调节器工程参数整定中,如果只按 4:1 衰减比进行整定,那么可以有很多对的比例度和积分时间同样能满足4:1 的衰减比,但是这些对的数值并不是任意的组合,而是成对的,一定的比例度必须与一定的积分时间组成一对,才能满足衰...