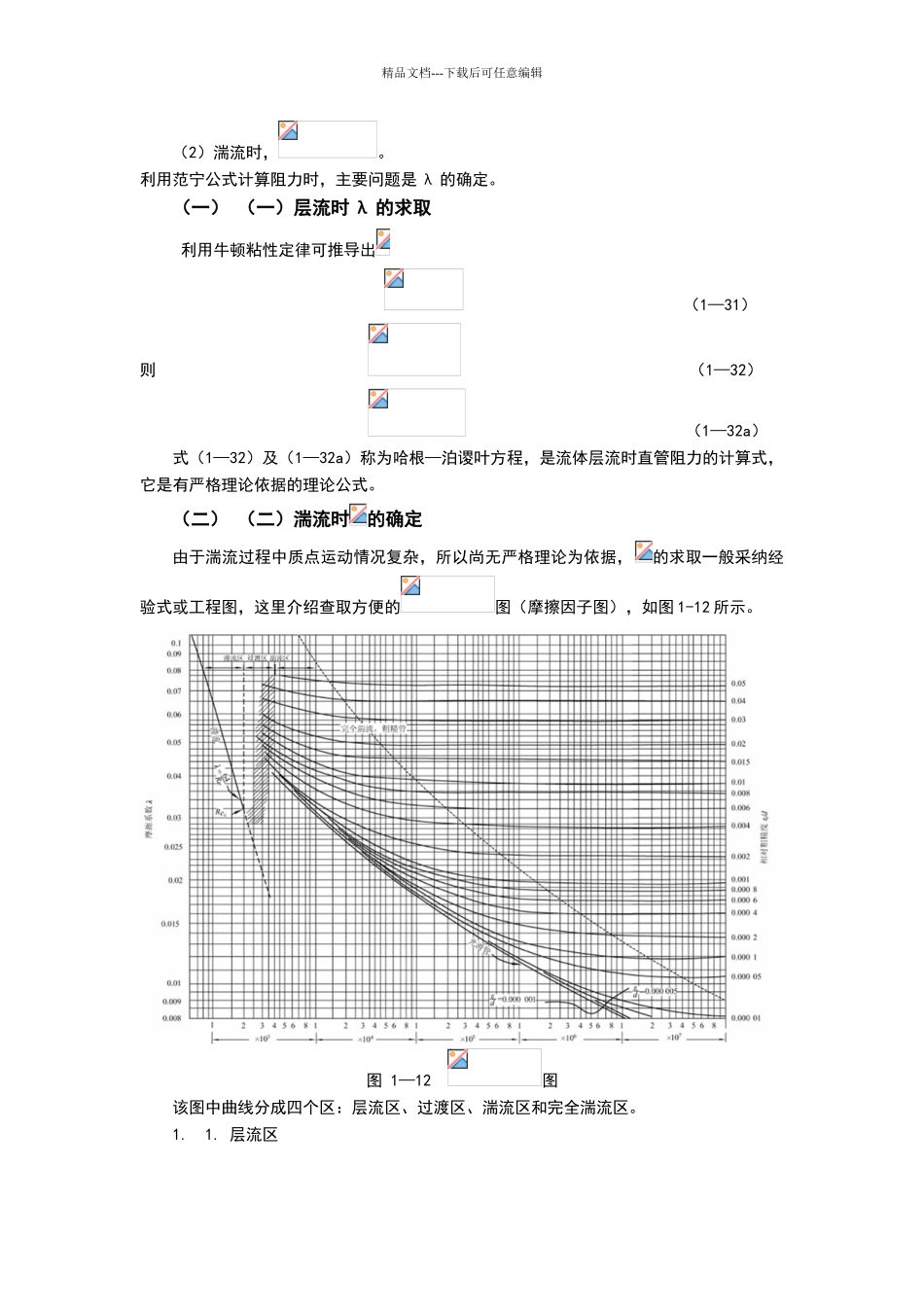
精品文档---下载后可任意编辑第四节 流体在管内流动阻力的计算壱、 一、压力降—流动阻力的表现 流动阻力产生的根本原因——流体具有粘性,所以流动时产生内摩擦力。如图 1—11所示,在贮槽下部连接的水平管上开两个小孔(A、B),分别插入两个竖直敞口玻璃管,调节出口阀开度,观察现象:1)1) 当 调 节 阀 关 闭 时 , 即 流 体 静 止 时 , A 、 B 管 中 液 面 高 度 与 贮 槽 液 面 平齐(可用静力学方程解释)。2)2)当打开阀门,流体开始流动后,发现 A 管液面低于贮槽液面,而 B 管液面又低于A 管液面。3)3)随着流速继续增大,A、B 管液面又继续降低,但 A 仍高于 B,分析如下:上述现象可用柏努利方程解释,分别取 A、B 点为截面,列柏努利方程: ++=Z2+++说明:(1)流体在无外 功加入,直径不变的水平管内流动时,两截面间的压差与流动阻力而引起的压强降数值相等。(2)若流体流动的管子是垂直或倾斜放置的,则两截面间的压差与流动阻力而引起的压强降数值不相等。弐、 二、流体在圆型直管中阻力损失的计算通式流体在圆管内流动总阻力分为直管阻力(又称沿程阻力)和局部阻力两部分。其中直管阻力是流体流经一定管径的直管时,由于流体的内摩擦而产生的阻力,这里讨论它的计算。范宁(Fanning)公式是描述各种流型下直管阻力的计算通式。 (1—30)或 (1—30a)式中 λ——摩擦系数,无因次。说明: (1)层流时,; 精品文档---下载后可任意编辑 (2)湍流时,。 利用范宁公式计算阻力时,主要问题是 λ 的确定。(一) (一)层流时 λ 的求取 利用牛顿粘性定律可推导出 (1—31)则 (1—32) (1—32a) 式(1—32)及(1—32a)称为哈根—泊谡叶方程,是流体层流时直管阻力的计算式,它是有严格理论依据的理论公式。(二) (二)湍流时的确定由于湍流过程中质点运动情况复杂,所以尚无严格理论为依据,的求取一般采纳经验式或工程图,这里介绍查取方便的图(摩擦因子图),如图 1-12 所示。图 1—12 图该图中曲线分成四个区:层流区、过渡区、湍流区和完全湍流区。1.1. 层流区精品文档---下载后可任意编辑即,在双数坐标中为一条直线,此时无关。2. 过渡区通常将湍流区的曲线延至此区伸查取值。3.湍流区(图中虚线以下区域) ,(1)(1)当相对粗糙度一定时, 增大而下降,当增至某一数值后,下降缓慢;(2)(2)当一定时,增大而增大。4.完全湍流...