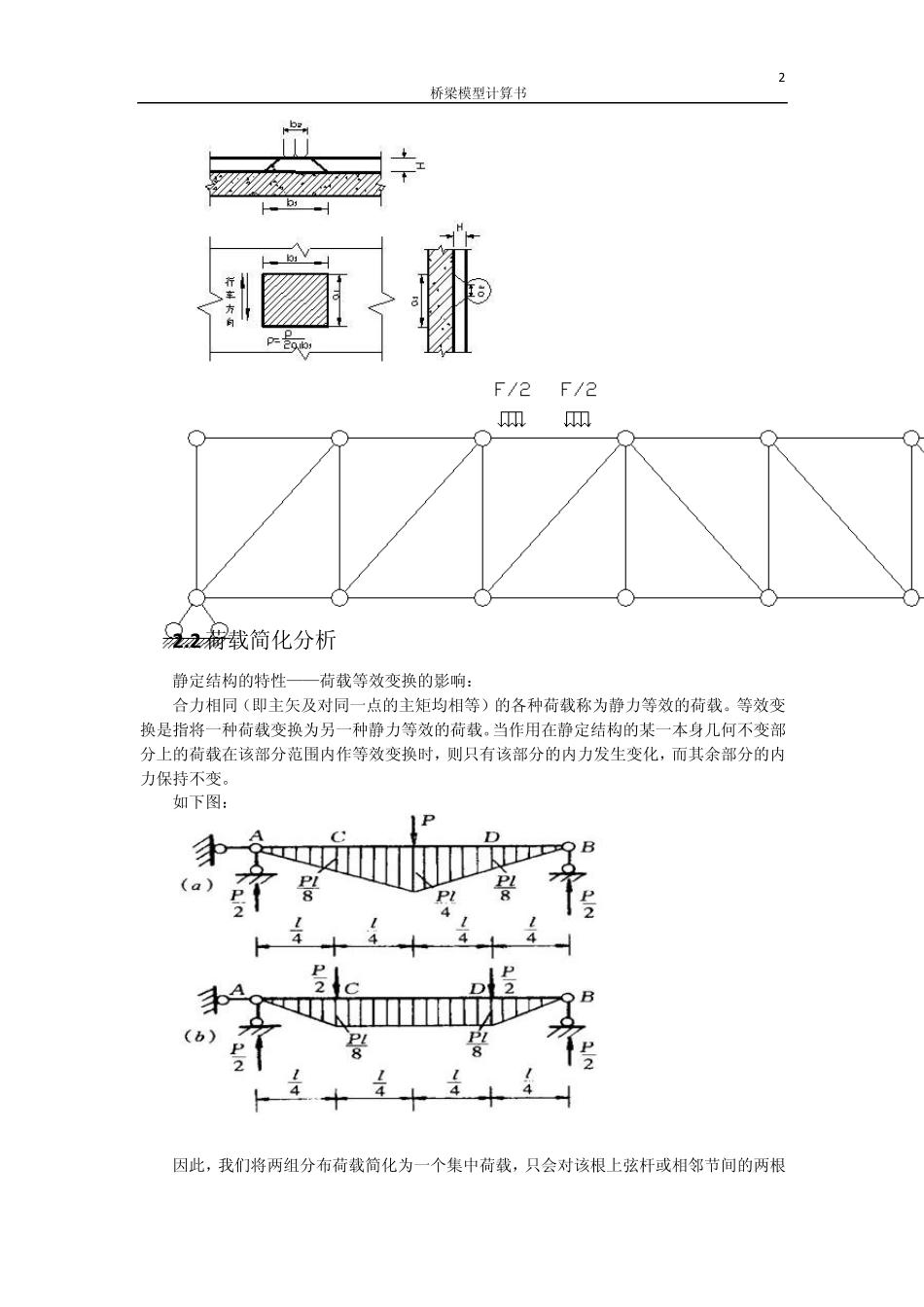
1 桥梁模型计算书 桥梁模型计算书 根据计算说明书,得到模型长度960mm,节间个数n=6,主桁高度h=160mm,斜腹杆角度α =45° 考虑到模型主要承受竖向的小车荷载,不需要承受纵向、横向荷载,也就是主要需要验算竖向荷载,进行主桁平面内的平面验算即可,采用手算。 在采用手算完成主体结构的设计之后,我组对本桥梁模型在 midas进行三维建模,检算平纵联和横向连接系形成的空间作用对结构承载力的提高,大约为 2 倍。 由于不知道棉线的强度,而且不确定棉线提供的预应力的效果,这里计算不予考虑,当作安全储备。 1. 计算模型 2. 荷载分析 轴距是??? 小于 160mm 2.1 实际工况 车轮荷载通过桥面结构传给主桁,是两部分分布荷载。大致如下: 2 桥梁模型计算书 2 .2 荷载简化分析 静定结构的特性——荷载等效变换的影响: 合力相同(即主矢及对同一点的主矩均相等)的各种荷载称为静力等效的荷载。等效变换是指将一种荷载变换为另一种静力等效的荷载。当作用在静定结构的某一本身几何不变部分上的荷载在该部分范围内作等效变换时,则只有该部分的内力发生变化,而其余部分的内力保持不变。 如下图: 因此,我们将两组分布荷载简化为一个集中荷载,只会对该根上弦杆或相邻节间的两根3 桥梁模型计算书 上弦杆有影响,对其他部分计算结果没有影响。 另外,每根上弦杆都需要承受弯矩和轴力的复合作用,因此,我们需要适当提高每根上弦杆的截面面积,提高承载力。 由于小车速度很慢,冲击系数取为1.0。 小车行驶到中间时,为最不利工况,杆件内力最大。 最终计算简图如下: 3 . 内力分析 进行手算,得到如下结果: 因此,下弦杆截面积应为竖腹杆的3 倍,斜腹杆的2.1 倍。 两种桐木条:粗木条6m m ×6m m ,细木条4.5m m ×3.5m m 。 进行组合得到: 杆件 选材 截面积(m m 2) 上弦杆 两根粗木条 72 下弦杆 两根粗木条 72 竖腹杆 一根细木条 15.75 斜腹杆 一根细木条 15.75 考虑到横联中使用的斜杆能够帮助传递竖向荷载,这里腹杆截面积较小。 4 桥梁模型计算书 4. 承载能力估算 初步的平面分析,认为控制结构强度的是中部的下弦杆。 根据《木结构设计规范》,木材强度在 10~20MPa 之间。 对中部的下弦杆进行计算,其中,木条抗压强度按 10MPa 计算。 21.5F=A=10M Pa72m m=720 N720F== 480 N1.5 承载能力估算为480N~960N。 5. 三维分析 5.1 三维 ...