求线面角的三种常见思路方法

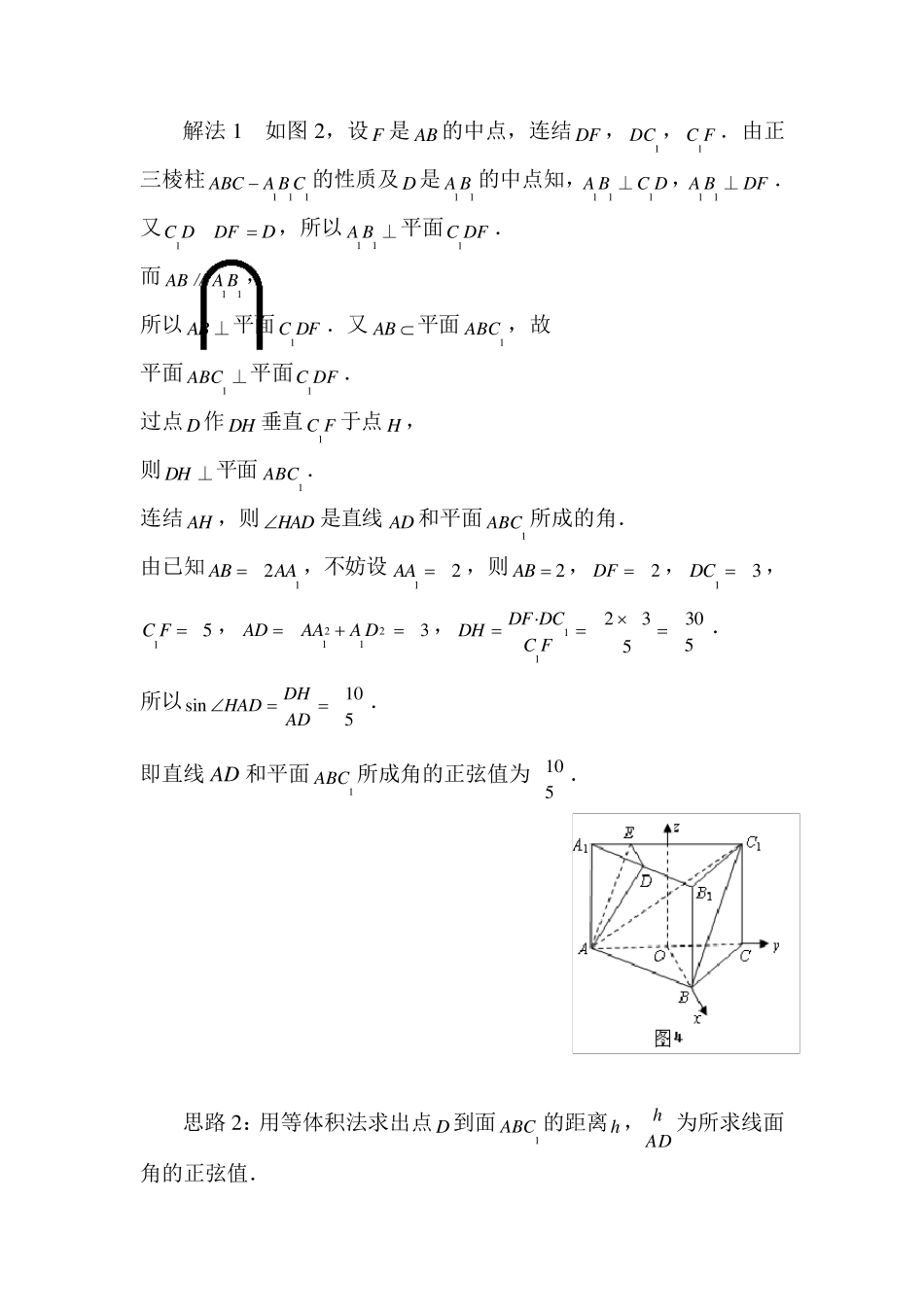
求线面角的三种常见思路方法 舒云水 本文以2009 年湖南卷理18 题为例，介绍求线面角的三种常见思路方法，并对这三种方法作比较分析﹒ 如图1，在正三棱柱111ABCA B C中，12ABAA，点D 是11A B 的中点，点E 在11AC 上，且DEAE⊥． （I）证明：平面ADE 平面11ACC A ； （II）求直线AD 和平面1ABC 所成角的正弦值． （Ⅰ）证明略． 下面主要谈（Ⅱ）小题的解法﹒ 思路1：直接作出线面角求解﹒ 分析：因为本题几何图形是特殊的几何体——正三棱柱，点D 在特殊位置上——线段11BA的中点，所以本题比较容易作出线面角﹒如图2，取 AB的中点F ，连结DF ，1DC ，FC1，则面1DFC面1ABC ，过 D作 FCDH1于 H ，则DH面1ABC ，连结 AH ，则HAD是AD和平面1ABC 所成的角﹒ 解法1 如图2，设F 是AB 的中点，连结DF ，1DC ，1C F ．由正三棱柱111ABCA B C的性质及D是11A B 的中点知，111A BC D⊥，11A BDF⊥． 又1C DDFD，所以11A B ⊥平面1C DF ． 而11ABA B∥， 所以AB⊥平面1C DF ．又AB 平面1ABC ，故 平面1ABC ⊥平面1C DF ． 过点D作 DH 垂直1C F 于点H ， 则 DH ⊥平面1ABC ． 连结AH ，则HAD是直线 AD 和平面1ABC 所成的角． 由已知12ABAA，不妨设12AA ，则2AB  ，2DF ，13DC ， 15C F ，2211ADAAA D3，11·233055DF DCDHC F． 所以10sin5DHHADAD． 即直线 AD 和平面1ABC 所成角的正弦值为 105 ． 思路 2：用等体积法求出点D到面1ABC 的距离h，ADh 为所求线面角的正弦值． 分析 如图3，连结DC1，BD，即得四棱锥1ABCD ．用等体积法，即DABCABCDVV11，容易求出点D 到平面1ABC 的距离h，ADh 为所求线面角的正弦值． 解法2：如图3，连结DC1，BD．因为平面111CBA平面1AB ，DC111BA ，所以DC1平面1AB ． 不妨设12AA ，则2AB  ，13DC ，611 BCAC，BDAD = 3 . 易求 2ADBS，51ABCS． 设 D在平面1ABC 内的射影为H ，hDH ，连结AH ，则HAD是直线AD 和平面1ABC 所成的角． 因为DABCABCDVV11，所以有 ABDABCSDCSh131311， 65h， 530h． 所以10sin5DHHADAD． 即直线AD 和平面1ABC 所成角的正弦值为105 ． 思路 3：坐标向量法． 解法3 如图4，设 O 是 AC 的中点，以O 为原点建立空间...