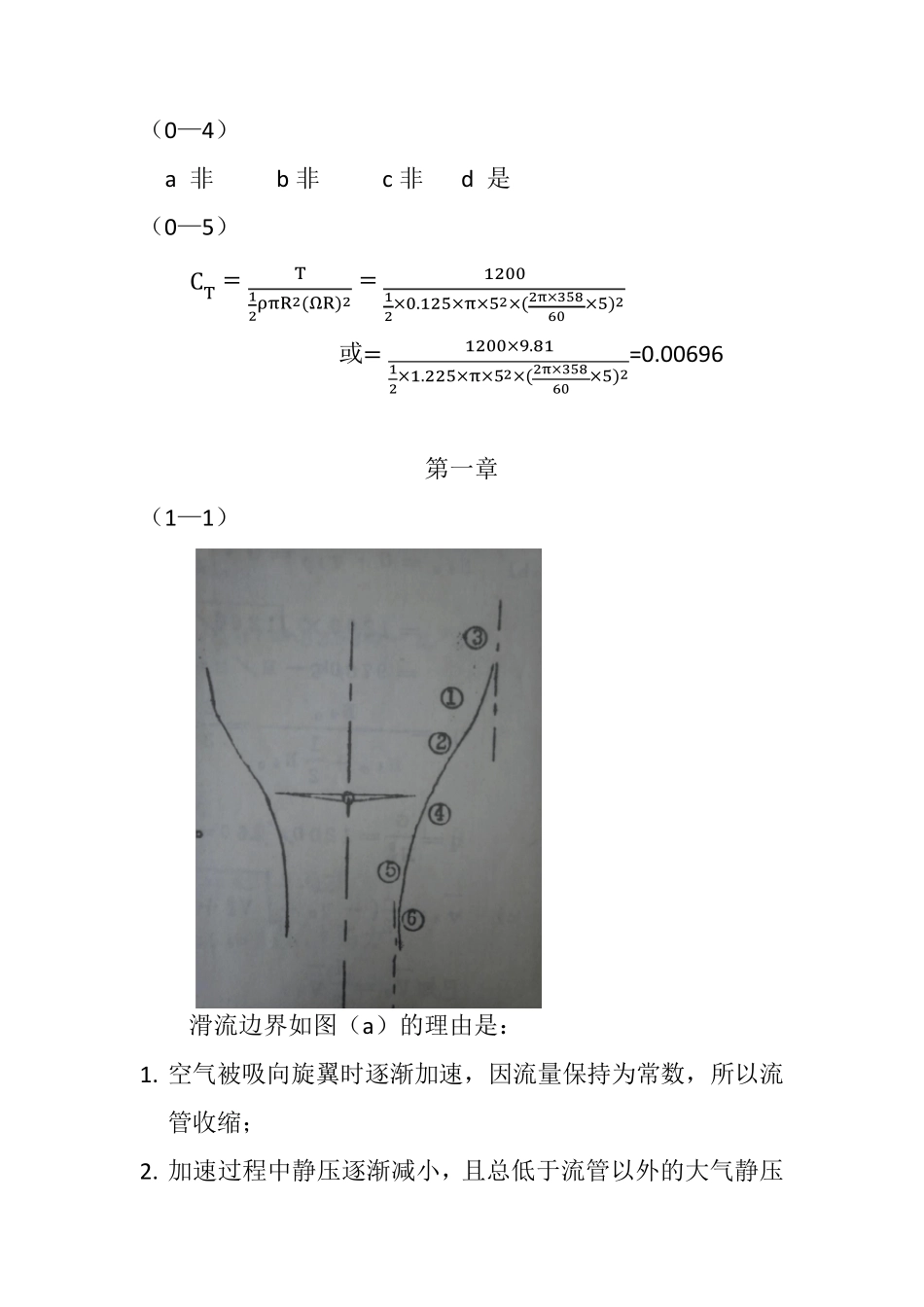
直升机空气动力学 习题解答 南京航空学院 一九九零年六月 绪论 (0—1) σ = kbπR =6×0.54π×18.9 2⁄ = 0.109 ΩR = 2πn60 × D2 = 2π(207 或 212)60× 18.92 = {204.8209.8M S⁄ M = ΩRa =1340 × {204.8209.8 = { 0.6020.617 (0—2) φ = φ7 + ∆φ(r̅ −0.7) = 11 −10(r̅ −0.7) = 18o −10r̅ 其中 r̅ = 0.7 , φ7 = 11o r̅ = 0.29 , φ根 = 15.1o r̅ = 0.1 , φ尖 = 8o (0—3) a 非 b 是 c 是 d 非 (0—4) a 非 b 非 c 非 d 是 (0—5) CT =T12 ρπR2 (ΩR)2 =12 0012 ×0.12 5×π×52 ×(2 π×3 586 0×5)2 或=12 00×9.8 112 ×1.2 2 5×π×52 ×(2 π×3 586 0×5)2 =0.00696 第一章 (1—1) 滑流边界如图(a)的理由是: 1. 空气被吸向旋翼时逐渐加速,因流量保持为常数,所以流管收缩; 2. 加速过程中静压逐渐减小,且总低于流管以外的大气静压强。内外压差使气体微团受到向内的法向力(向心力),所以流线向内凹; 3. 上游无限远处,v = v0 ,静压与大气压相同,所以流体的渐近线为竖直线; 4. 桨盘处,气流在此被加压,流线有拐点; 5. 气流经旋翼加压后,将逐渐加速,所以流管收缩;又因滑流内静压高于外界大气压,因而流管边界线向外凹; 6. 下游无限远处,v = v0 + v20 压强为大气压,所以流管边界线的渐近线为竖直线。 (1—2) a. v10 = √G2ρπR2K =√1200 (2 × 0.125× π × 52 × 0.92)⁄= 8.15m s⁄ b. Ni0 = G× v10 = G√Gκ2ρπR2 = 1200× √1200 (2 × 0.125× π × 52 × 0.92)⁄ = 130.4马力 η0 =Ni0Ni0+0.5Ni0= 23 = 66.7% q =GNM0 = 1200 260⁄= 4.6 公斤 马力⁄ c. v1̅ = 0.5(− v0̅̅̅+ √v̅02 + CT κ⁄ ) 已知 v0̅̅̅ = 13 v10̅̅̅̅ ,而v10̅̅̅̅ = 12 √CTκ , CT =G12ρπR2(ΩR)2 =0.00696 所以 v10̅̅̅̅ = 12 √0.00696 0.92⁄= 0.0435 V1̅̅̅ = 12 (− 0.04353+ √(0.04353)2 + 0.00696 0.92⁄) = 0.0368 Ni = Gv1̅ ΩR= 1200× 0.0368× 187 = 110 马力 N = Ni + N0 + N⊥ 式中 N0 = 12 Ni0 = 65.2 马力 N⊥ = G13 v10 = 43.5 马力 N = 110+ 65.2 + 43.5 = 218....