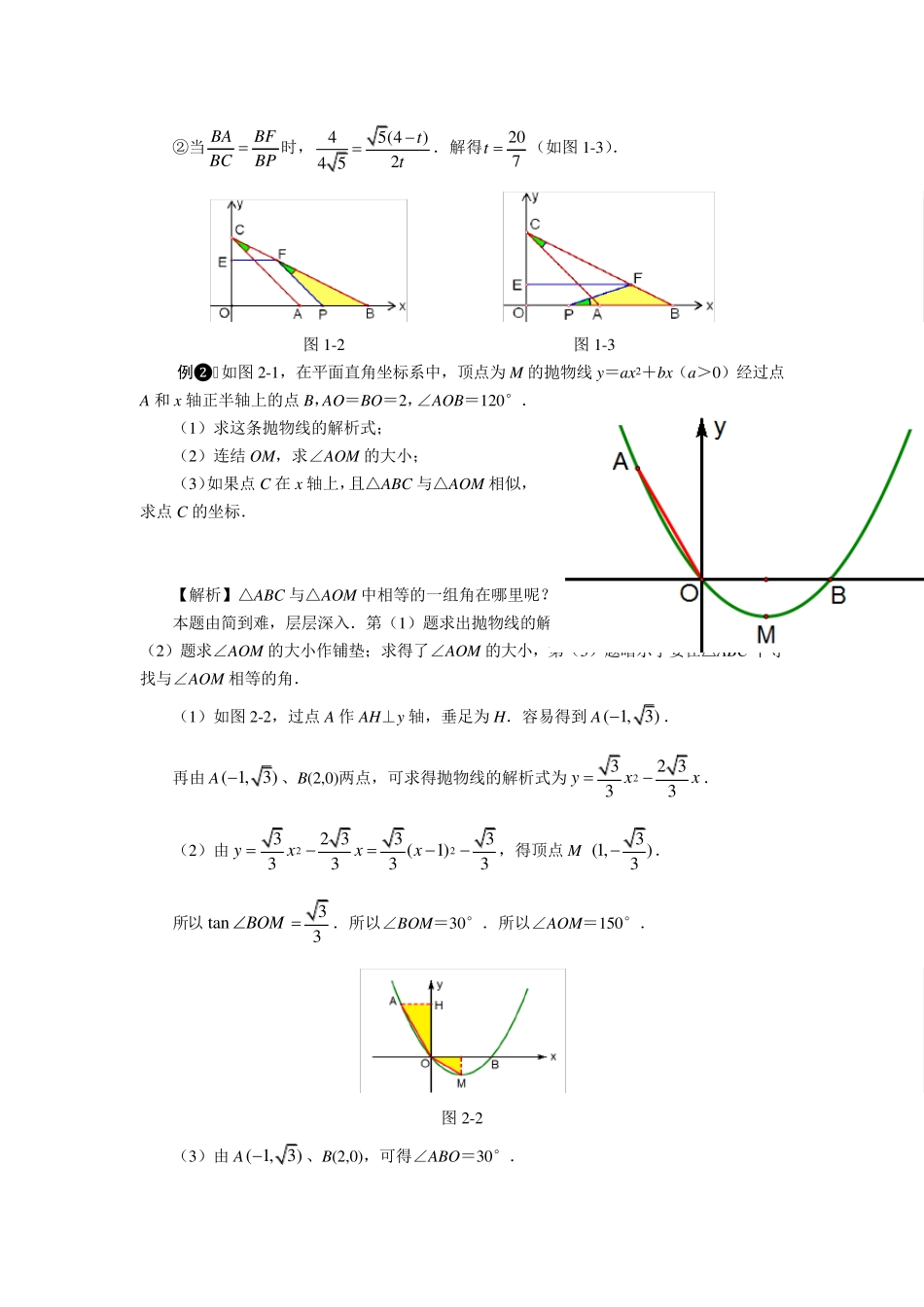
中考数学压轴题解题策略(2) 相似三角形的存在性问题解题策略 《挑战压轴题·中考数学》的作者 上海 马学斌 专题攻略 相似三角形的判定定理有 3 个,其中判定定理 1 和判定定理 2 都有对应角相等的条件,因此探求两个三角形相似的动态问题,一般情况下首先寻找一组对应角相等. 判定定理 2 是最常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验,如例题1、2、3、4. 应用判定定理 1 解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等,如例题6. 应用判定定理 3 解题不多见,如例题5,根据三边对应成比例列连比式解方程(组). 例题解析 例❶ 如图 1-1,抛物线213482yxx与 x 轴交于 A、B 两点(A 点在 B 点左侧),与y 轴交于点 C.动直线 EF(EF//x 轴)从点 C 开始,以每秒 1 个单位的速度沿 y 轴负方向平移,且分别交 y 轴、线段 BC 于 E、F 两点,动点 P 同时从点 B 出发,在线段 OB 上以每秒2 个单位的速度向原点 O 运动.是否存在 t,使得△BPF 与△ABC 相似.若存在,试求出 t的值;若不存在,请说明理由. 图 1-1 【解析】△BPF 与△ABC 有公共角∠B,那么我们梳理两个三角形中夹∠B 的两条边. △ABC 是确定的.由213482yxx,可得 A(4, 0)、B(8, 0)、C(0, 4). 于是得到 BA=4,BC=4 5 .还可得到12CECOEFOB. △BPF 中,BP=2t,那么 BF 的长用含 t 的式子表示出来,问题就解决了. 在 Rt△EFC 中,CE=t,EF=2t,所以5CFt. 因此4 555(4)BFtt. 于是根据两边对应成比例,分两种情况列方程: ①当 BABPBCBF时,424 55(4)tt.解得43t (如图 1-2). ②当BABFBCBP时,45(4)24 5tt.解得207t (如图1-3). 图1-2 图1-3 例❷ 如图2-1,在平面直角坐标系中,顶点为M 的抛物线y =ax 2+bx(a>0)经过点A 和x 轴正半轴上的点B,AO=BO=2,∠AOB=120°. (1)求这条抛物线的解析式; (2)连结 OM,求∠AOM 的大小; (3)如果点C 在x 轴上,且△ABC 与△AOM 相似,求点C 的坐标. 图2-1 【解析】△ABC 与△AOM 中相等的一组角在哪里呢? 本题由简到难,层层深入.第(1)题求出抛物线的解析式,得到顶点M 的坐标,为第(2)题求∠AOM 的大小作铺垫;求得了∠AOM 的大小,第(3)题暗示了要在△ABC 中寻找与∠AOM...