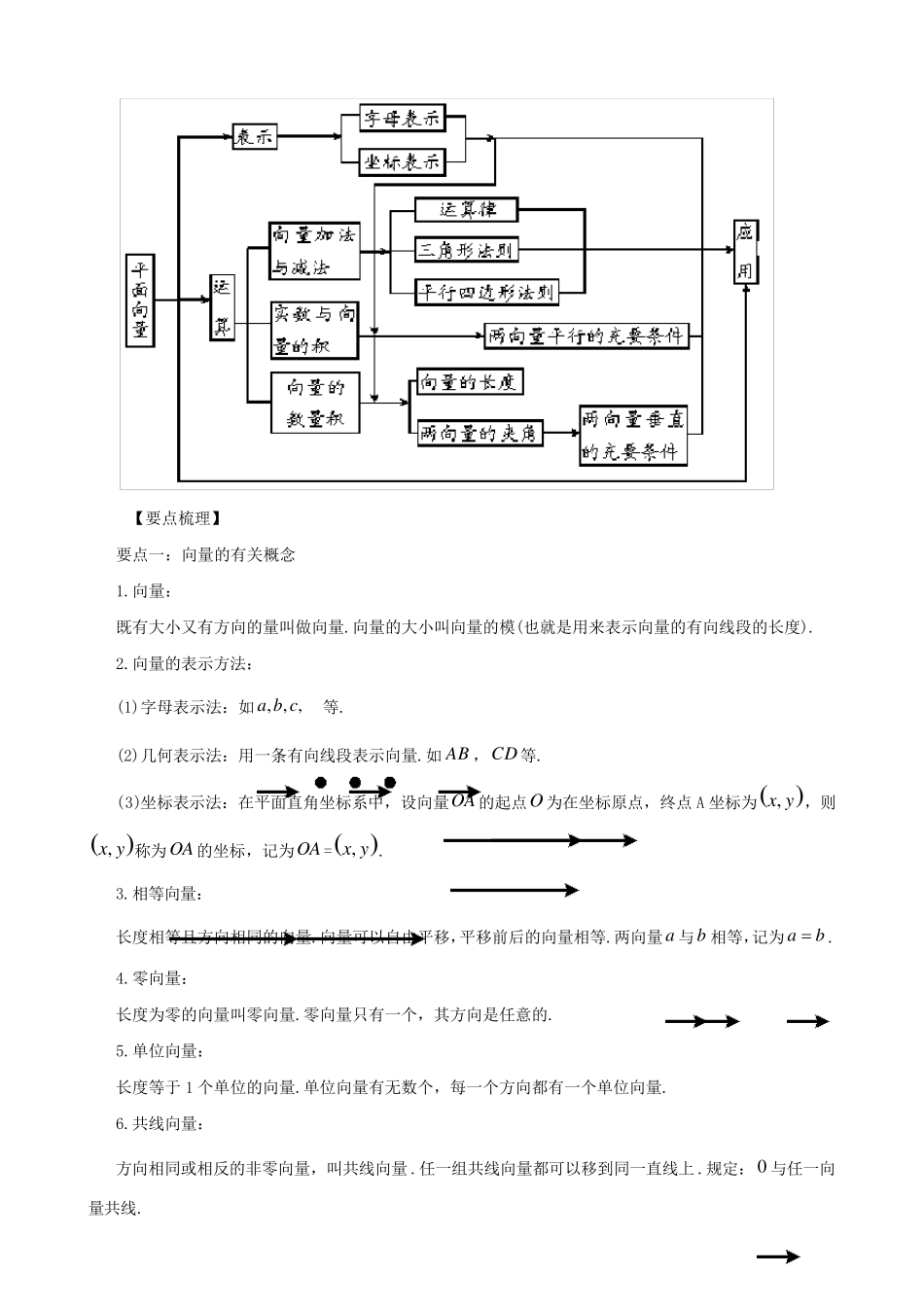
《平面向量》全章复习与巩固 编稿:孙永钊 审稿:王静伟 【学习目标】 1.平面向量的实际背景及基本概念 通过力和力的分析等实例,了解向量的实际背景,理解平面向量和向量相等的含义,理解向量的几何表示; 2.向量的线性运算 (1)通过实例,掌握向量加、减法的运算,并理解其几何意义; (2)通过实例,掌握向量数乘的运算,并理解其几何意义,以及两个向量共线的含义; (3)了解向量的线性运算性质及其几何意义. 3.平面向量的基本定理及坐标表示 (1)了解平面向量的基本定理及其意义; (2)掌握平面向量的正交分解及其坐标表示; (3)会用坐标表示平面向量的加、减与数乘运算; (4)理解用坐标表示的平面向量共线的条件. 4.平面向量的数量积 (1)通过物理中"功"等实例,理解平面向量数量积的含义及其物理意义; (2)体会平面向量的数量积与向量投影的关系; (3)掌握数量积的坐标表达式,会进行平面向量数量积的运算; (4)能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系. 5.向量的应用 经历用向量方法解决某些简单的平面几何问题、力学问题与其他一些实际问题的过程,体会向量是一种处理几何问题、物理问题等的工具,发展运算能力和解决实际问题的能力. 【知识网络】 【要点梳理】 要点一:向量的有关概念 1.向量: 既有大小又有方向的量叫做向量.向量的大小叫向量的模(也就是用来表示向量的有向线段的长度). 2.向量的表示方法: (1)字母表示法:如 , , ,a b c等. (2)几何表示法:用一条有向线段表示向量.如 AB ,CD 等. (3)坐标表示法:在平面直角坐标系中,设向量OA 的起点O 为在坐标原点,终点 A 坐标为,x y ,则,x y 称为OA 的坐标,记为OA =,x y . 3.相等向量: 长度相等且方向相同的向量.向量可以自由平移,平移前后的向量相等.两向量a 与b 相等,记为ab. 4.零向量: 长度为零的向量叫零向量.零向量只有一个,其方向是任意的. 5.单位向量: 长度等于 1 个单位的向量.单位向量有无数个,每一个方向都有一个单位向量. 6.共线向量: 方向相同或相反的非零向量,叫共线向量 .任一组共线向量都可以移到同一直线上 .规定:0 与任一向量共线. 注:共线向量又称为平行向量. 7.相反向量: 长度相等且方向相反的向量. 要点二、向量的运算 1.运算定义 运 算 图形语言 符号语言 坐标语言 加法与减法 OA +OB...