离散数学第二次作业

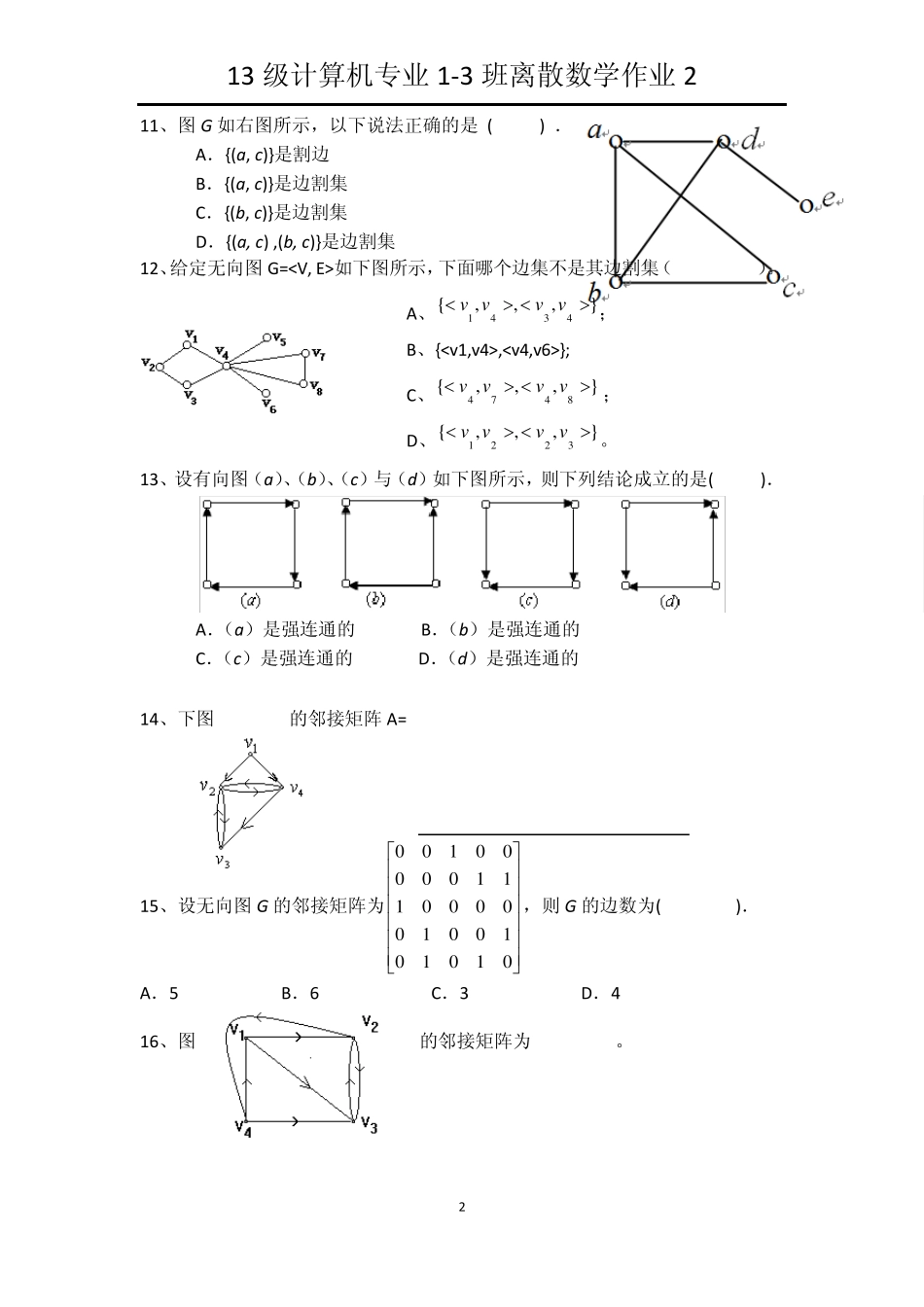
13 级计算机专业1-3 班离散数学作业2 班级 姓名 学号 成绩 一、 图的概念、连通性与矩阵表示 选择/填空题 1、 任何 n个节点 m条边的图 G = (V,E) , 边数与顶点度数的关系是 。 2、任一有向图中，度数为奇数的结点有( )个。 3、n 阶完全图 Kn 的边数为 。 4、n个结点的有向完全图边数是( )，每个结点的度数是( )。 5、已知图 G 中有 1 个 1 度结点，2 个 2 度结点，3 个 3 度结点，4 个 4 度结点，则 G 的边数是 ． 6、下面四组数能构成无向图的度数列的有( )。 A、 2,3,4,5,6,7； B、 1,2,2,3,4； C、 2,1,1,1,2； D、 3,3,5,6,0。 7、设无向图 G有 16条边且每个顶点的度数都是 2，则图 G有( )个顶点。 (1) 10 (2) 4 (3) 8 (4) 16 8、在有 n个顶点的连通图中，其边数（ ）。 (1) 最多有 n-1条 (2) 至少有 n-1 条 (3) 最多有 n条 (4) 至少有 n 条 9、如右图 相对于完全图 K5 的补图为（ ）。 10、给定无向图 G 如下图所示，下面给出的结点集子集中，不是点割集的为（ ）． A．{b, d} B．{d} C．{a, c} D．{b, e} 13 级计算机专业1-3 班离散数学作业2 2 11、图 G 如右图所示，以下说法正确的是 ( ) ． A．{(a, c)}是割边 B．{(a, c)}是边割集 C．{(b, c)}是边割集 D．{(a, c) ,(b, c)}是边割集 12、给定无向图 G=如下图所示，下面哪个边集不是其边割集（ ）。 A、； B、{,}; C、； D、。 13、设有向图（a）、（b）、（c）与（d）如下图所示，则下列结论成立的是( )． A．（a）是强连通的 B．（b）是强连通的 C．（c）是强连通的 D．（d）是强连通的 14、下图 的邻接矩阵 A= 15、设无向图 G 的邻接矩阵为0101010010000011100000100，则 G 的边数为( )． A．5 B．6 C．3 D．4 16、图 的邻接矩阵为( )。 },,,{4341vvvv},,,{8474vvvv},,,{3221vvvv13 级计算机专业1-3 班离散数学作业2 3 A、；B、；C、；D、。 综合题 17、设 G=，V={ v1，v2，v3，v4，v5}，E={ (v1,v3)，(v2,v3)，(v2,v4)，(v3,v4)，(v3,v5)，(v4,v5) }，试 (1) 给出 G 的图形表示； (2) 写出其邻接矩阵； (3) 求出每个结点的度数； (4) 画出其补图的图形． 18、已知：D=，V={1,2,3,4,5}，E={<1,2>,<1,4>,...