空间几何体表面积与体积公式大全

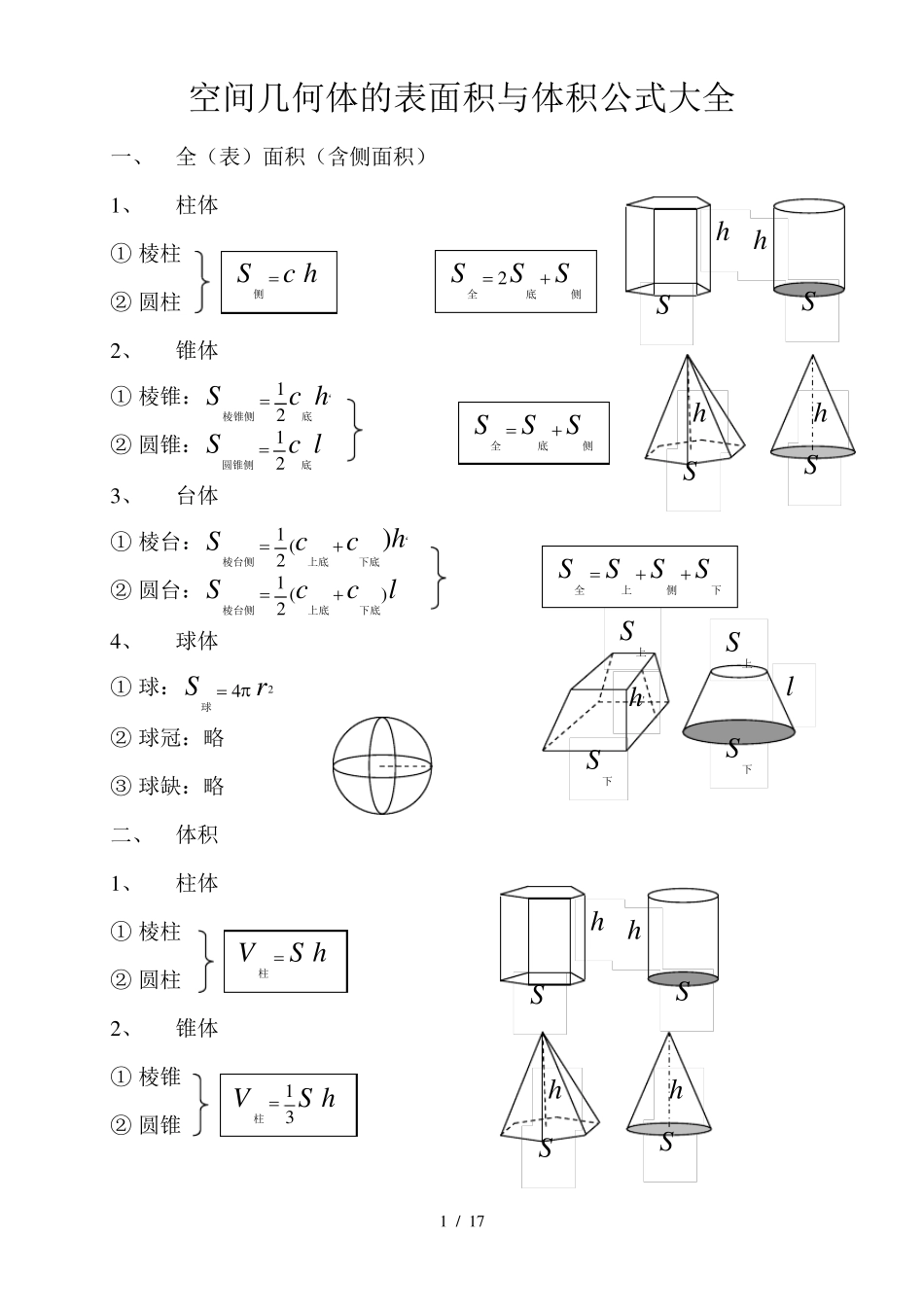
1 / 1 7 空间几何体的表面积与体积公式大全 一、 全（表）面积（含侧面积） 1 、 柱体 ① 棱柱 ② 圆柱 2 、 锥体 ① 棱锥：hcS‘底棱锥侧21 ② 圆锥：lcS底圆锥侧21 3 、 台体 ① 棱台：hccS)(21‘下底上底棱台侧 ② 圆台：lccS)(21下底上底棱台侧 4 、 球体 ① 球： rS24 球 ② 球冠：略 ③ 球缺：略 二、 体积 1 、 柱体 ① 棱柱 ② 圆柱 2 、 锥体 ① 棱锥 ② 圆锥 h' S上 S上 l S下 S下 hcS侧 SSS侧底全 2 SSS侧底全 SSSS下侧上全 hSV柱 hSV31柱 h S h S h S h S h S h S h S h S 2 / 1 7 3 、 台体 ① 棱台 ② 圆台 4 、 球体 ① 球：rV334 球 ② 球冠：略 ③ 球缺：略 说明：棱锥、棱台计算侧面积时使用侧面的斜高h'计算；而圆锥、圆台的侧面积计算时使用母线l 计算。 三、 拓展提高 1 、 祖暅原理：（祖暅：祖冲之的儿子） 夹在两个平行平面间的两个几何体，如果它们在任意高度上的平行截面面积都相等，那么这两个几何体的体积相等。 最早推导出球体体积的祖冲之父子便是运用这个原理实现的。 2 、 阿基米德原理：（圆柱容球） 圆柱容球原理：在一个高和底面直径都是 r2的圆柱形容器内装一个最大的球体，则该球体的全面积等于圆柱的侧面积，体积等于圆柱体积的32 。 )(3122rrrrhV下下上上圆台 )(31SSSShV下下上上台 h h' S上 S上 l S下 S下 3 / 1 7 分析：圆柱体积：rrhSVr3222)(圆柱 圆柱侧面积：rhcSrr242)2(圆柱侧 因此：球体体积：rrV3334232球 球体表面积： rS24 球 通过上述分析，我们可以得到一个很重要的关系（如图） + = 即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和 3 、 台体体积公式 公式： )(31SSSShV下下上上台 证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD。 延长两侧棱相交于一点P 。 设台体上底面积为S上，下底面积为S下 高为h 。 易知：PDC∽ PAB，设hPE1， 则hhPF1 由相似三角形的性质得：PFPEABCD  E F A B C D P 4 / 17 即：hhhSS11下上(相似比等于面积比的算术平方根) 整理得：SShSh上下上1 又因为台体的体积=大锥体体积—小锥体体积 ∴hSSShhShhSV下上下上下台...