第8章无源网络传递函数的综合第12节内容总结(6页)

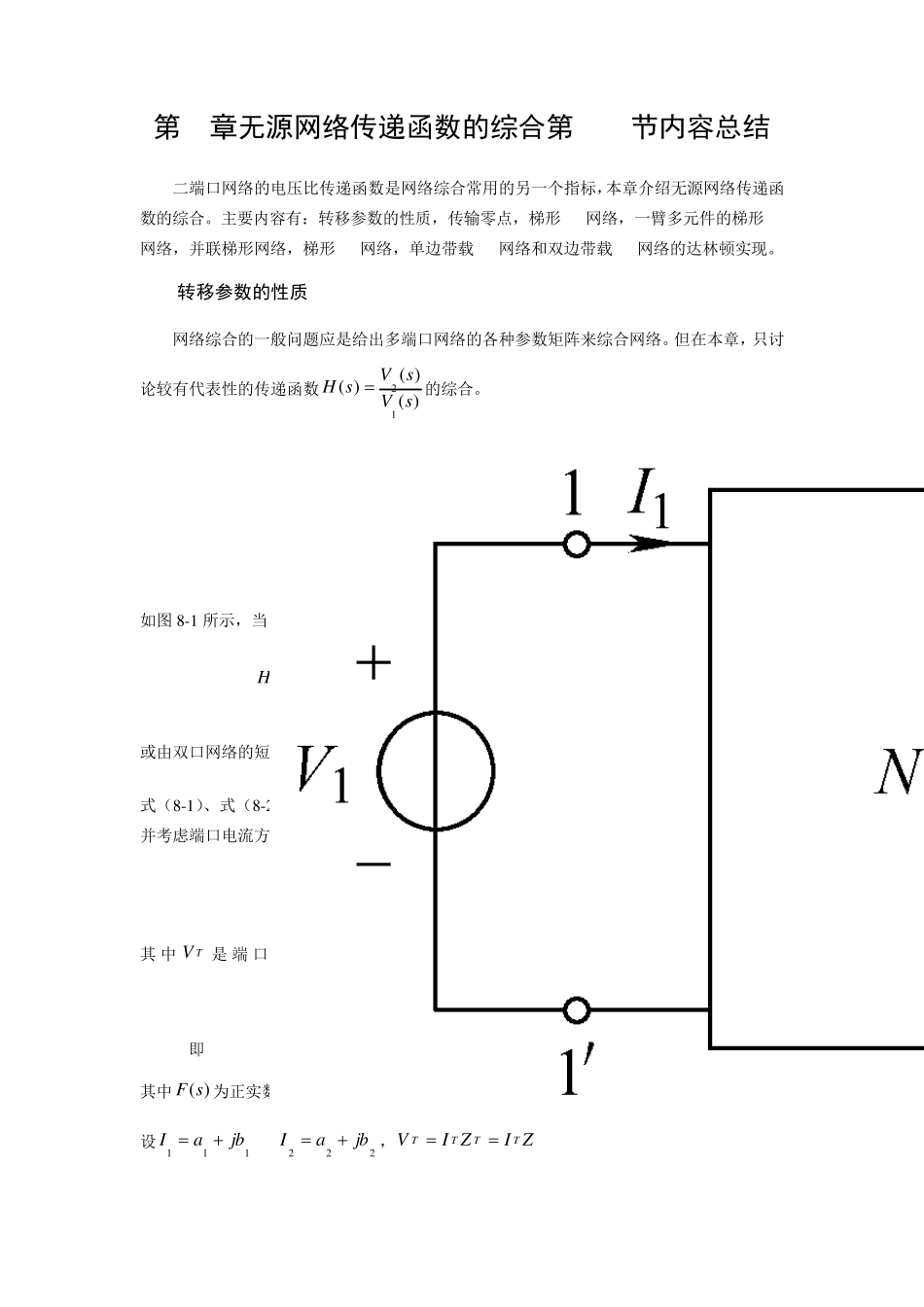
第8章无源网络传递函数的综合第1-2节内容总结 二端口网络的电压比传递函数是网络综合常用的另一个指标，本章介绍无源网络传递函数的综合。主要内容有：转移参数的性质，传输零点，梯形RC网络，一臂多元件的梯形RC网络，并联梯形网络，梯形LC网络，单边带载LC网络和双边带载LC网络的达林顿实现。 8.1 转移参数的性质 网络综合的一般问题应是给出多端口网络的各种参数矩阵来综合网络。但在本章，只讨论较有代表性的传递函数)()()(12sVsVsH的综合。 图8 -1 利用开路参数计算传递函数 如图8 -1 所示，当02 I，由双端口网络的开路参数方程可得： )()()()()(1 12 112sZsZsVsVsH （8 -1 ） 或由双口网络的短路参数方程可得： )()()()()(2 22 112sYsYsVsVsH （8 -2 ） 式（8 -1 ）、式（8 -2 ）的分母是策动点函数。为讨论上述转移参数的特性，应采用特勒定理并考虑端口电流方向得 jbjjTIVIVIVIV32211 （8 -3 ） 其 中TV是端口的电压向 量 ，I 是端口电流 流 向 的共 轭 ，式（8 -3 ）右 边为)()(1)()(000sFsVsssMsF （8 -4 ） 即 )(sFIV T （8 -5 ） 其中)(sF为正实数。端口电压向量 ZIV  （8 -6 ） 设111jbaI 222jbaI，ZIZIVTTTT 其中 Z 是双端口的开路参数矩阵，将上式和)()(2 11 2sZsZ代入式(8 -5 )得 )()(221212 1222 2211 112 1221 21222 2211 1sFbbaaZIZIZIZIIZIIZIZIZIIVTT （8 -7 ） 因此得 )(2)()()()(2121222 2211 12 1bbaaIsZIsZsFsZ （8 -8 ） 设)(sF、)(1 1 sZ、)(2 2 sZ、)(2 1 sZ在 jw 轴上某极点处留数分别为k 、1 1k、2 2k、2 1k显然k 、1 1k、2 2k各自大于等于零 ，故有 )(221212122222111bbaakIkIkk （8 -9 ） 其中212121baI，222222baI，代入式（8 -9 ）后得 0)2()2(2 222212 11 1212 222212 11 121kbbbkkbkaaakka a 、b 为任意实数时均需满足，，所以每个括号项分别均应为非负。其中第一个括号项可以改写为 1 12 2211 12 1221221 1)(2)(kkaakkaaak （8 -1 0 ） 或 21 12 11 12 221 12 121221 1)()(kkkkkkaaak （8 -1 1 ） 电流的实部1a 、2a 可正可负，即使在01 12 121 kkaa时，式（8 -1 1 ）...